Rchaeology

Wir haben eine ganze Menge Gefäße, haben Maße abgenommen und sehen nun, daß sich keine “natürlichen” Gruppen absetzen, sondern alles irgendwie mit allem zusammenhängt. Dabei wollen wir doch eine Typologie erstellen! Wir brauchen also ein Werkzeug, daß Ähnliches zueinander sammelt und Verschiedenes trennt. Clustern kann uns dabei helfen. Im Folgenden skizziere ich eine (von vielen) Möglichkeiten – das Modellbasierte Clustern.

Als Datengrundlage nutzen wir einige Maße von schnurkeramischen Gefäßen aus Mitteldeutschland (SKGefaesse).

keramik <- read.table(file="SKGefaesse.txt",header=TRUE,dec=",",sep="\t")

Schauen wir uns die Daten zunächst einmal an:
Übersicht:
pairs(keramik[,3:9],pch=15,cex=0.3,col=rainbow(12)[as.numeric(keramik$art)],lower.panel=NULL)

Detailbeispiel:
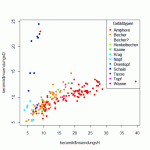
plot(keramik$muendungsH,keramik$muendungsD,col=rainbow(12)[as.numeric(keramik$art)],pch=16)
legend(title="Gefäßtypen","topright",legend=levels(keramik$art),col=rainbow(12)[1:12],pch=16)

Streudiagramm Rohdaten Gefäßhöhe:Mündungsweite

Man sieht im Diagramm Gefäßhöhe zu Mündungsweite schön, wie sich die offenen Gefäßformen (Schalen, Wannen) von den geschlossenen absetzen. Gleichzeitig fällt hier aber, wie auch in allen anderen Kombinationen aus Streudiagrammen auf, daß sich letztere, also Amphoren, Becher usw. kaum voneinander unterscheiden.

Das bedeutet nicht, daß unsere a priori getroffene Klassifizierung nichts taugt – wir sehen lediglich, daß sich die Gefäßklassen in den aufgenommenen Maßen kaum unterscheiden. Also noch mehr Maße aufnehmen, in der Hoffnung irgendwann genug Daten gesammelt zu haben? Auch das wäre vorschnell, denn je mehr Maße wir verwenden, umso redundanter wird unser Datensatz, wir hätten also noch mehr Arbeit für wenig Zugewinn.

Unser Ziel also: Finde eine stimmige Unterteilung der geschlossenen Gefäßformen!

Dazu löschen wir zunächst die Schalen und Wannen (enthalten aufgrund ihrer einteiligen Gefäßform sowieso nur unvollständige Messdaten).

keramikber<-na.omit(keramik)

Jetzt haben wir die Absolutmaße für unsere Gefäßpopulation, aber das genügt noch nicht, denn der Algorithmus “sieht” die Gefäße ja nicht, sondern nur die Maße, die er wiederum stur miteinander vergleicht. So auch weitspannende Maße wie zB die Gefäßhöhe mit kleineren Gefäßdimensionen wie zB dem kleinsten Gefäßdurchmesser. Für den Algorithmus könnte dadurch die Gefäßhöhe auch absolut variabler erscheinen als der kleinste Durchmesser und damit stärker als andere Maße das Ergebnis beeinflussen. Uns interessiert aber die Variabilität aller Maße – vielleicht sind es ja gerade die kleinen Dimensionen, die die Gefäße voneinander unterscheiden. Also standardisieren wir unsere Werte zunächst (=normalisieren, =Z-Scores, wer mehr dazu wissen möchte, kann in der Wikipedia nachschauen). Alternativ könnten wir alle Maße relativ zu einem Gefäßmaß, z.B. der Höhe ausdrücken also z.B. MündungsD/Höhe; MaxD/Höhe usw. aber das könnte in bestimmten Fällen wieder zu Verzerrungen führen. Bleiben wir für heute bei der Standardisierung:

keramikber_scal<-keramikber # neuer Datensatz zur Weiterverarbeitung
keramikber_scal[,3:9]<-scale(keramikber_scal[,3:9]) # Spalten 3-9 (=Maße) werden standardisiert

Gruppenanzahl und Modell

Clustern bedeutet, wir unterteilen unsere Population in, ja, wieviele Gruppen eigentlich? Auch hier hilft uns R! Mit mclustBIC werden verschiedene G, d.h. Gruppenanzahlen, durchgespielt. Aber nicht nur das. Die Cluster können verschiedene Formen haben. Im zweidimensionalen Streudiagramm z.B. runde oder ellipsenförmige Wolken bilden, und in höher dimensionierten Räumen entsprechende Formen bilden (in unserem Fall z.B. siebendimensional, weil wir sieben Maße untersuchen). Siebendimensionale Punktwolken… nun, auch diese verschiedenen Formen werden mittels verschiedener Modelle durchprobiert:

Modellbasiertes Clustern. Ergebnisdiagramm für zehn Modelle und ein bis 16 Gruppen.

library("mclust")        # Paket vorher laden - notfalls installieren
kk_BIC<-mclustBIC(keramikber_scal[,3:9],G=1:16)  # probiert mit 1-16 möglichen Unterteilungen
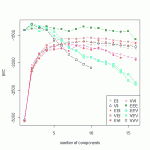
plot(kk_BIC)

Die Darstellung sieht wild aus, liest sich aber einfach: Der höchste Peak gewinnt! In unserem Fall also Modell “VEV” bei zwei “number of components”. Das nutzen wir für den nächsten Schritt, das Clustern:

kk_clus2<-Mclust(keramikber_scal[,3:9], G=2,modelnames="VEV")

Nur zwei Cluster??? Das ist in der Tat ein wenig mager. Schauen wir mal, wie sich die morphognostische Klassifizierung mit diesen Clustern verträgt:

table(keramikber_scal$art,kk_clus2$classification)

                1  2
  Amphore      60 21
  Becher        2 49
  Becher?       0  1
  Henkelbecher  0  1
  Kanne         2  7
  Krug          0  1
  Napf          0  0
  Ösentopf      0  0
  Schale        0  0
  Tasse         0  3
  Topf          3  1
  Wanne         0  0

Unsere 81 Amphoren teilen sich also mit drei Vierteln gegen ein Viertel auf beide Cluster auf. Die Becher scheinen eigener und konzentrieren sich stark im zweiten Cluster. Amphoren scheinen in den verwendeten Maßen also variabler als Becher.

Aber wir hatten, nach der Bereinigung, acht morphognostische Klassen geschlossener Gefäßformen, probieren wir also die Clusterei mal mit G=8. Das BIC-Diagramm hilft uns: bei acht Gruppen ist das Modell “EEE” am besten geeignet.

kk_clus8<-Mclust(keramikber_scal[,3:9], G=8,modelnames="EEE")
table(keramikber_scal$art,kk_clus8$classification)

Es wird deutlich, daß sich die Amphoren auf weitere Cluster verteilen, die Becher aber in nur zwei Clustern massiv auftreten. Dabei wird ein Cluster fast ausschließlich von Bechern besetzt, während dem anderen Cluster auch häufig Amphoren zugeschlagen wurden. Die Erhöhung der Clusterzahl würde zur weiteren Aufspaltung, wahrscheinlich zuvörderst der Amphoren, schließlich aber auch der Becher führen, und zu guter letzt würde jeder Cluster nur ein Gefäß enthalten.

Dendrogramm

Soweit gehen wir nicht, stattdessen werfen wir einen Blick auf die Ähnlichkeit der erstellten Cluster untereinander. Dazu berechnen wir die Positionen (=Mittelwerte für jede Variable der enthaltenen Gefäße) der Cluster und anschließend deren Abstand:

kk_clus_means<-aggregate(keramikber_scal[,3:9], by=list(cluster=kk_clus8$classification),FUN=mean)
kk_clus_dist <- dist(kk_clus_means[,2:8], method = "euclidean")

Die Abstandsmatrix wird erneut zum Clustern (dieses Mal hierarchisch agglomerativ) verwendet und dann ein Baumdiagramm erstellt.

kk_clus_dendro <- hclust(kk_clus_dist, method="ward") # hierarchisches Clustern unserer Cluster
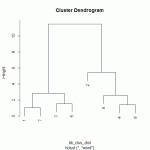
plot(kk_clus_dendro) # Dendrogramm

Dendrogramm mit acht modellbasiert ermittelten Clustern.

Das Baumdiagramm weist auf die uns schon bekannte Zweiteilung hin; die oberste Gabelung ist sehr hoch, dh die Gruppierung auf dieser Ebene – die Separierung der Cluster 1, 3, 5 und 7 (alles Amphoren!) – ist sehr stark.

Aus den Ergebnisse kann also geschlossen werden, daß die aufgenommenen Maße gar nicht so invariat sind, wie es zunächst den Anschein hatte und eine Aufgliederung in Untergruppen durchaus sinnvoll erscheint. Ferner ist die morphognostische Ansprache – natürlich auch nur im Hinblick auf die verwendeten Meßwerte – nicht nur nützlich, sondern es zeigt sich auch, daß die Amphoren formenvariabler als die Becher sind. Nichtsdestotrotz läßt sich die morphognostische Klassifizierung mit unseren Meßwerten nicht vollständig erklären. Dazu wären nicht unbedingt weitere Maße nötig, vielmehr würden Angaben zur Anzahl und Lage der Henkel (wie in der guten alten R-losen Zeit) genügen.

Wer sich noch intensiver mit den Clustern beschäftigen möchte, kann sich zB das erste Diagramm in diesem Artikel anzeigen lassen, aber jetzt nach Clustern eingefärbt:

plot(keramikber$muendungsH,keramikber$muendungsD,col=rainbow(2)[kk_clus2$classification],pch=16) # die Zwei-Cluster-Version

plot(keramikber$maxD_H,keramikber$muendungsD,col=rainbow(8)[kk_clus8$classification],pch=16) # acht Cluster
legend(title="Cluster","bottomright",legend=c(1:8),col=rainbow(8)[1:8],pch=16)

PS: Graphische Umsetzung der Gefäßmaße

Schnurkeramische Gefäße. Silhouetten, nach Clustergruppen geordnet und eingefärbt.

Im Artikel über das Erstellen eigener Funktionen habe ich Euch gezeigt, wie Ihr die Messwerte zur Darstellung von Gefäßsilhouetten nutzen könnt – und das wäre doch ganz praktisch zur optischen Qualitätsprüfung von Clusterergebnissen!

Ladet die beiden Funktionen potplot() und potblock() in den R-Speicher und probiert folgende Zeilen zur Darstellung des Ergebnisses mit zwei Clustern:

ordne<-keramikber[order(kk_clus2$classification),]

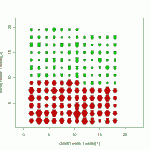
potblock(ordne[,3:9],farbe=kk_clus2$classification[rownames(ordne)]+1)

Schon wird deutlich, daß die Gefäße in erster Linie nach Größe klassifiziert werden, anhand der Silhouetten erkennt man aber auch, daß sich im ersten Cluster (“rot”) mehr Amphoren und im zweiten, “grünen” Cluster mehr Becher befinden. Da das Gefäßvolumen offensichtlich mit dem Gefäßtyp assoziiert ist, läßt sich allerdings nicht quantifizieren, inwieweit der Algorithmus auch anhand der Meßwert-Variabiliät gruppiert hat – und genau diese Ungewissheit über den Anteil der zur Gruppierung führenden Faktoren ist ein Nachteil der Clusteranalyse. Die Beurteilung des Ergebnisses kann letztlich nur intuitiv erfolgen.

Zum Schluß noch ein Tipp und vielleicht eine Anregung zum Selbertüfteln: Skaliert man die Gefäßmaße vor der Clusterei anhand der Volumina ergibt sich eine konsistentere Gruppierung. Nicht ganz so kompliziert und womöglich auch zu einer guten Gliederung führend könnte die Skalierung anhand der größten Gefäßmaße, also maxD und muendungsH erfolgen.