Funktionen selbst gebaut – Potplot
Häufig genutzte Codeschnipsel lassen sich in selbst erstellten Funktionen unterbringen. Ich zeige Euch, wie Ihr Gefäßumrisse anhand der aufgenommenen Maße darstellt, diese Gefäßskizzen z.B. in Diagrammen unterbringt – und wie Ihr dieses kleine Paket in einer einzigen Programmzeile unterbringen könnt.
Die Idee kam mir beim Schreiben des Cluster-Artikels. Es wäre doch praktisch, wenn man, anstatt in den Kopien zu wühlen und die Gefäßzeichnungen von Hand zu sortieren, sich die Topfumrisse vom Rechner ausgeben lässt; anhand der aufgenommenen Maße müßte das doch möglich sein?!
Vorarbeit – Funktionsinhalt wird erstellt
Wir benötigen also zunächst wieder den Beispieldatensatz mit den schnurkeramischen Gefäßen:
keramik <- read.table(file="SKGefaesse.txt",header=TRUE,dec=",",sep="\t")
keramikber<-na.omit(keramik) # nur die mehrgliedrigen Gefäße bleiben übrig
Nun probieren wir, ob die Maße wirklich zur Rekonstruktion des Gefäßumrisses nützlich sind. Zunächst eine kurze Erläuterung der Maße:
muendungsD- MündungsdurchmessermuendungsH- Höhe des GefäßesminD- kleinster Durchmesser (außer evtl. Mündung oder Boden)minD_H– Höhe des kleinsten DurchmessersmaxD- größter Durchmesser (außer evtl. Mündung oder Boden)maxD_H– Höhe des größten DurchmessersbodenD– Bodendurchmesser
Aus diesen Maßen lassen sich die Lagen der Meßpunkte – und zwar relativ zueinander – rekonstruieren. Wollen wir ein Gefäß darstellen, benötigen wir genau diese Information. Laßt uns nun ein Gefäß vom Computer zeichnen. Und zwar am besten so, daß der Nullpunkt in der Gefäßmitte liegt (das vereinfacht uns die späteren Schritte).
Also, wo liegt nun z.B. der obere Gefäßrand, wenn der Nullpunkt in der Gefäßmitte liegen soll? Auf halber Gefäßhöhe nach oben. Der Gefäßboden entsprechend auf halber Gefäßhöhe nach unten. Mit den Horizontalmaßen (den Durchmessern) verfahren wir ebenso, d.h. wir tragen sie jeweils zur Hälfte links und rechts vom Nullpunkt ab. Konkret liegt der X-Wert der linken Gefäßoberkante also bei 0-muendungsD*0.5 und ihr Y-Wert bei muendungsH*0.5. Da die Gefäßumrisse an der Mittellinie spiegelsymmetrisch sind, brauchen wir die X-Werte nur einmal zu berechnen und dann einmal links von der Nullinie (0-X) und einmal rechts davon (0+X) abzutragen. Zur Darstellung benutzen wir die Funktion polygon(x,y), die kein eigenes Graphikfenster öffnet, wir müssen vorher also ein leeres Diagramm erstellen:
x1<-0.5*keramikber$muendungsD[1]; y1<-0.5*keramikber$muendungsH[1] # Punkte werden berechnet
x2<-0.5*keramikber$minD[1]; y2<-keramikber$minD_H[1]-0.5*keramikber$muendungsH[1]
x3<-0.5*keramikber$maxD[1]; y3<-keramikber$maxD_H[1]-0.5*keramikber$muendungsH[1]
x4<-0.5*keramikber$bodenD[1]; y4<-0-0.5*keramikber$muendungsH[1]
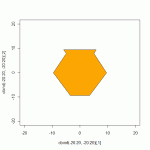
plot(cbind(-20:20,-20:20),type="n",asp=1) # Vorbereitung: ein leeres Diagramm
polygon(x=c(x1,x2,x3,x4,-x4,-x3,-x2,-x1),y=c(y1,y2,y3,y4,y4,y3,y2,y1),col="orange")
Das Polygon wird “oben rechts” begonnen, nach unten bis zum Boden fortgesetzt (x1,y1 bis x4,y4), wechselt dann in die “linke” Hälfte des Umrisses (d.h. negative X-Werte) und fährt dort von unten nach oben fort (-x4,y4 bis -x1,y1). Die Funktion schließt den Umriß automatisch (zeichnet zum Schluß also noch einen Strich zurück zum Anfangspunkt).
Wir haben aber 150 Gefäße! Und die sollen alle gemäß ihrer individuellen Maße skizziert werden, möglichst in einer frei wählbaren Anordnung und in verschiedenen Farben…
Auslagern in eine Funktion
Wir werden die obigen Zeilen nicht 150Mal wiederholen. Stattdessen parken wir den Code in einer Funktion. Dann können wir, wie bei allen anderen R-Funktionen auch, mit einer Zeile und ein paar Parametern, alle Töpfe in einer Graphik unterbringen.
Funktionen werden ähnlich wie Variablen definiert – mit einem Namen; diese Bezeichnung sollte möglichst eindeutig, nicht zu lang und v.a. noch nicht vergebenen sein; wie immer gilt auch hier: auf Groß- und Kleinschreibung achten! Funktionsargumente, also Informationen, die der Funktion übergeben werden, folgen dem Namen in runden Klammern “()”. Der Funktionsinhalt wird, daran anschließend, mit geschweiften Klammern “{}” umgeben. Das Einrücken des Funktionsinhaltes bringt noch ein paar Ästhetikpunkte (und macht den Code übersichtlicher).
meine_funktion <- function(argument1,argument2=0,argument3=0) {
Anweisung1;
Anweisung2;
}
Argumente! Das sind die Informationen, die die Funktion individualisieren und z.B. Koordinaten, Farbwerte, Größen – also die Variablen. Diese Variablen bekommen einen “lokalen” Namen, d.h. die Namen gelten nur in der Funktion. Sollen die Argumente optional sein, d.h. nicht unbedingt beim Funktionsaufruf bestimmt werden müssen, dann können sie mit Standardwerten versehen werden. Im obigen Beispiel haben argument2 und argument3s olche Standardwerte, nur argument1 muß vom Nutzer übergeben werden, damit die Funktion lauffähig wird.
Beim Funktionsaufruf werden die Werte den Funktionsargumenten entweder per “=” zugewiesen
x<-2
y<-"hallo"
z<-5
meine_funktion(argument1=x,argument2=y,argument3=8) # das ist die sichere Variante
oder aber kurz und knapp – dann aber in der gleichen Reihenfolge wie in der Funktionsdefinition!
meine_funktion(x,y,z) # kürzer, aber die Gefahr der Verwechslung besteht
Beide Varianten können auch gemischt werden:
meine_funktion(x,argument3=z,argument2=y)
Für unsere Funktion wollen wir folgende Argumente verwenden:
- Gefäßmaße, Argument:
gefaesse - Koordinaten – wo soll das Gefäß dargestellt werden, Argument:
x, y - Skalierungsfaktor, für den Fall, daß wir den Maßstab anpassen müssen, Argument:
skal - Farbe, Argument:
farbe
Um schön übersichtlich zu programmieren, übergeben wir die sieben Gefäßmaße nicht einzeln, sondern verpackt als Dataframe:
potplot<-function (gefaesse,x=0,y=0,skal=1,farbe="red") { # gefaesse[1]=muendungsD,2=muendungsH,3=minD,4=minD_H,5=maxD,6=maxD_H,7=bodenD
m<-as.vector(gefaesse,mode="numeric") # Dataframe wird als Vector aufgetrennt
x1<-0-0.5*m[1]; y1<-0.5*m[2] # nun stehen die Maße einzeln zur Verfügung
x2<-0-0.5*m[3]; y2<-m[4]-0.5*m[2]
x3<-0-0.5*m[5]; y3<-m[6]-0.5*m[2]
x4<-0-0.5*m[7]; y4<-0-0.5*m[2]
polygon(x=c(x1,x2,x3,x4,-x4,-x3,-x2,-x1)*skal+x,y=c(y1,y2,y3,y4,y4,y3,y2,y1)*skal+y,col=farbe)
}
Fügt den Funktionscode in R ein (copy & paste) – achtet darauf, daß auch die letzte Zeile (geschweifte Klammer) mit [Eingabe] abgeschlossen wird. Die Funktion ist nun im Programmspeicher vorhanden und nach Bedarf abrufbar.
Wenn schon ein Graphikfenster geöffnet ist, probiert folgendes:
plot(cbind(-20:20,-20:20),type="n",asp=1) # wieder zunächst ein leeres Graphikfenster
potplot(gefaesse=keramikber[2,3:9])
Damit werden die Spalten drei bis neun aus der zweiten Zeile von keramikber ausgewählt, d.h. die Maße des zweiten Gefäßes, und an die soeben eingegebene Funktion potplot() übergeben. Die Silhouette wird im Graphikfenster rot gefüllt über dem Koordinatenursprung (0,0) gezeichnet.
Als nächsten Schritt hätten wir gern mehrere Gefäße in einer Darstellung. Dazu schreiben wir noch eine Funktion, die sich ihrerseits der Funktion potplot() bedient, denn selbstverständlich können Funktionen auch Funktionen aufrufen, die wieder Funktionen… naja, und so weiter.
Noch eine Funktion
Die nächste Funktion soll mehrere Gefäße möglichst kompakt und übersichtlich darstellen. Die Form der Wahl ist in diesem Fall das Quadrat, dessen Seitenlänge die neue Funktion anhand der Anzahl der darzustellenden Gefäße ausrechnet. Nach der Berechnung der Darstellungsgröße wird jede Zeile des erhaltenen Dataframes, d.h. jedes Gefäß einzeln aufgerufen und mitsamt seiner Position an potplot() übergeben. So teilen sich beide Funktionen die Arbeit der Positionsberechnung einerseits und der Darstellung der einzelnen Gefäße andererseits.
potblock<-function (gefaesse,skal=0.05,farbe=0) {
zeilen<-round(sqrt(length(gefaesse[,1]))) # wieviele Zeilen & Spalten sind am kompaktesten (Quadrat)?
weite<-zeilen*1.5+3 # Größe des Plotfeldes wird berechnet
plot(cbind(1:weite,1:weite),type="n",asp=1) # leeres Plotfeld darin dann...
for (i in 1:length(gefaesse[,1])) { # ...die Gefäße
j<-((i-1)%%zeilen+1)*1.5 # mit "%%" wird modulo gerechnet
k<-(floor(abs(((i-1)/zeilen)))+1)*1.5
potplot(gefaesse=gefaesse[i,1:7],x=j,y=k,skal=skal,farbe=farbe[i]) # mit farbe[i] wird die individuelle Farbgebung möglich
}
}Jetzt können wir uns alle Gefäße auf einmal anzeigen lassen!
potblock(keramikber[,3:9])
Abgesehen von den offensichtlichen Messfehlern (v.a. in der vorletzten Zeile) fallen gleich die Größen- und sogar Formunterschiede auf. – Und das, obwohl wir nur insgesamt sechs Maße pro Gefäß verwenden.
Mit dieser Darstellungsform können wir “archäologisch experimentieren”, und uns z.B. die Gefäße nach der Höhe geordnet und entsprechend der morphognostischen Typenansprache eingefärbt anzeigen lassen:
ordne<-keramikber[order(keramikber$muendungsH),]
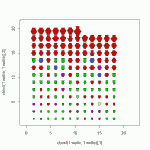
potblock(ordne[,3:9],farbe=as.numeric(ordne$art)+1) # +1, um schwarze Gefäße zu vermeiden
Das ordnen anhand der Spalte (=Vektor) muendungsH erfolgt mittels order(). Die Zeilenindices werden in der geordneten Reihenfolge beim Aufruf des Dataframe keramikber verwendet, der wiederum in der gewünschten Anordnung in der Variable ordne gespeichert wird. Der Farbparameter benötigt eine Zahl, also werden die morphologischen Typansprachen mit as.numeric() umgewandelt.
Das Ergebnis zeigt, daß es sich bei den größten Gefäßen ausschließlich um Amphoren (Rot) handelt, während die kleinsten meistens als Becher (grün) angesprochen wurden.
Rückgabe von Werten aus Funktionen
Selbstverständlich können Funktionen außer der graphischen Ausgabe auch andere Informationen an den Benutzer zurückmelden. Ein einzelner Wert, nämlich der jeweils letzte, der in der Funktion erzeugte, kann einfach per Aufruf zurückgegeben werden, z.B.
quadrat <- function(x) {
x^2
}
quadrat(3)
Sollen hingegen mehrere Werte zurückgegeben werden, müssen wir diese zu einem einzigen Objekt zusammenfassen. Viele Funktionen nutzen dafür die Form der Liste.
quadrat <- function(x,y) { return(list(x^2,y^2)) # verpackt die Ergebnisse in einer Liste und gibt sie zurück } quadrat(3,4) # Funktionsaufruf für Textausgabe k<-quadrat(3,4)# so speichert man die Funktionsausgabe in einem Objekt (...also wie bekannt...) k[[1]] # und so ruft man die einzelnen Objekte aus der Überobjekt (Liste) ab k[[2]]