Die Chord-Distanz: ein Distanzmaß zur Messung der Unähnlichkeit von Typenvergesellschaftungen
Dieser Artikel beschreibt das Anwendungsfeld, die Berechnung und die Eigenschaften der sog. Chord-Distanz, im Folgenden Chorddistanz geschrieben. Zahlreiche multivariate Verfahren, u. a. Gruppenbildungsverfahren (Clusteranalysen), basieren auf der Messung der Unähnlichkeit zwischen den Objekten eines multivariaten Datensatzes. In der Archäologie haben solche Datensätze häufig die Form von Typenvergesellschaftungstabellen oder sog. Kontingenztabellen. In den Zeilen solcher Tabellen stehen die untersuchten Fälle – etwa Befunde -, und in den Spalten die absolute Häufigkeit eines Typs. Die Chorddistanz dient zur Messung der Unähnlichkeiten zwischen den Fällen solcher Tabellen und erlaubt dadurch die Anwendung diverser multivariater Verfahren auf die Tabelle.
Die Chorddistanz benutzt als Grundlage der (Un-)Ähnlichkeitsmessung im Prinzip die Zeilenprozentwerte der verglichenen Fälle (Zeilen). Sie beachtet Unterschiede bei den Zeilensummen nicht. Bei der Messung der Unähnlichkeit kann es sein, dass die Unterschiede zwischen den Häufigkeiten präsenter Typen genauso bewertet werden sollen, wie die zwischen Typen, die bei einem Fall (mehrfach) vorhanden und bei einem anderen abwesend sind (vgl. u. 2.6. Distanzmaßsymmetrie). Wenn eine solche Bewertung gewünscht ist, ist die Chorddistanz ungeeignet. Wenn hingegen, was in der Archäologie üblicher ist, nur die Unterschiede zweier Fälle in Bezug auf die anwesenden Typen zur Messung ihrer (Un-)Ähnlichkeit dienen sollen, dann ist die Chorddistanz eines der zu empfehlenden Distanzmaße.
Nach der Ermittlung der Chorddistanz erhält man als Ergebnis eine Distanzmatrix (vgl. u. 2.7.). Distanzmatrizen sind der Ausgangspunkt für viele verschiedene multivariate (geostatistische) Methoden wie Ballungsanalysen (Clusteranalysen), Ordinationen durch nichtmetrische multidimensionale Skalierung (NMDS), Testen zur Auswirkung von Gruppenzugehörigkeiten auf die Ähnlichkeiten der Fälle (Verweis zur R-Funktion im Paket vegan), der Analyse der Beziehung zweier Typenvergesellschaftungstabellen mit den gleichen Fällen mittels Manteltesten oder der Analyse von Abundanzunähnlichkeiten in Abhängigkeit von der geografischen Entfernung mittels Mantelkorrelogrammen. Die Chorddistanz bietet eine ideale Basis dafür, solche Verfahren auf archäologische Typenvergesellschaftungstabellen anzuwenden. Solche weitere Auswertungen sind nicht Gegenstand dieses Artikels – einzelne werden vielleicht einmal Thema eines zukünftigen Blogeintrages sein. Alle diese Verfahren können in R gerechnet werden. Wer Anregungen zu ihrer Anwendung in R sucht findet beim Informationsdient R-seek Informationen dazu. Auf der Internet-Seite von R gibt es auch einen eigenen Überblick zu diversen Clusterfunktionen in R-Paketen.
Eine .pdf-Version dieses Blog-Beitrages ist hier zu erhalten.
1. Einführung zur Chorddistanz
– 2.3. Distanz- und Ähnlichkeitsmaß
– 2.4. Variablenart und Distanzmaß
– 2.6. Symmetrie eines Distanzmaßes
3. Euklidische Distanz und Abundanzen
4. Berechnung der Chorddistanz
5. Zum geometrischen Verständnis der Chorddistanz
– 6.2. Einlesen einer Abundanztabelle aus einem “Spreadsheet”
– 6.3. Berechnung mit dem Paket ‘vegan’
– 6.4. Berechnung mit anderen Paketen
7. Zusammenfassung Chorddistanz
9. Überblick über verwendete R-Befehle
1. Einführung zur Chorddistanz
Die Chorddistanz wurde 1967 von dem mittlerweile emeritierten Ökologieprofessor Laszlo Orloci (*1932) an der Universität von West-Ontario in London/Ontario, Kanada, entwickelt. Ihr Name, “chord” ist Englisch für Kreissehne, leitet sich aus ihrer Berechnung ab (s. u.). Sie ist ein in der Ökologie weitverbreitetes Maß zur Messung der Unähnlichkeit, der sog. Distanz, von Objekten anhand einer multivariaten Information über ihre Zusammensatzung.
Das Maß zählt in der Ökologie zu den Standardmaßen für die Erfassung von Unähnlichkeiten bei Abundanzen. Beispielsweise wird es im ökologischen Standardlehrbuch der Gebrüder Legendre als ein Distanzmaß für Vergesellschaftungstabellen empfohlen. Auch in anderen Wissenschaften wie beispielsweise in der Genetik wird es für vergleichbare Zwecke eingesetzt. Dort wird mit der Chord-Distanz die genetische Unähnlichkeit von Individuen gemessen. In der Genetik wie in der Ökologie soll in der Regel nur, wie in der Archäologie üblicherweise auch, das gemeinsame Vorhandensein von Eigenschaften die Grundlage der Unähnlichkeitsmessung bilden. Die Chorddistanz arbeitet auf dieser Basis. Diese Eigenschaft macht sie speziell für die Archäologie interessant.
Vor einigen Jahren wurde von Legendre und Gallagher entdeckt, dass eine Zwischenstufe bei der Berechnung der Chorddistanz das Potenzial besitzt, Typenvergesellschaftungstabellen als eine multivariate Ansammlung metrischer Variablen abzubilden. Dadurch werden Abundanzen für Ordinationsmethoden auf der Basis der euklidischen Distanz, wie etwa der Hauptkomponentenanalyse (PCA) nutzbar. Dieser Aspekt wird bei Legendre und Gallagher vertieft.
2. Einführung Distanzmaß
2.1. Grundlagen
Archäologische Typenvergesellschaftungstabellen haben in der Ökologie eine direkte Entsprechung. Dort heissen sie Abundanztabellen (vgl. u. 2.5.). Aus methodischer Sicht wäre es sinnvoll, in der Archäologie auch diese Bezeichnung zu verwenden, weil auf diese Weise Verwechslungsgefahren verringert und Übertragungen von Methoden erleichtert werden. Ein Ansatz für die Auswertung eines solchen multivariaten Datensatzes beruht nun auf der Messung der Übereinstimmung zwischen je zwei Fällen (Zeilen) der Tabelle. Grundsätzlich könnte man entweder den Grad der Übereinstimmung oder den Grad der Nicht-Übereinstimmung mit einem Maß messen. Der Grad in dem zwei Zeilen nicht übereinstimmen bzw. sich unterscheiden wird als Distanz bezeichnet. Solche Distanzen dienen zahlreichen multivariaten Verfahren als Basis für eine weitere Untersuchung der Fallbeziehung. Sie erlauben auch die Anwendung von Methoden, die Beziehungen zwischen den Fällen weiteren und weiteren Informationen (Variablen) zu den Fällen verbinden können. Auf diese Weise lässt sich beispielsweise überprüfen, ob eine archäologische Unterteilung der Fälle tatsächlich sinnvolle Gruppen erzeugt.
Für die Messung der Distanz zweier Fälle (Zeilen) gründet auf dem folgenden Prinzip. Es wird jeweils Zelle für Zelle der Wert des einen Falles mit dem Wert des anderen Falles verglichen. Abschließend werden alle Einzelvergleiche gebündelt und ein (!) zusammenfassendes Maß für die Distanz berechnet. Die multivariate Information über die Unähnlichkeit zweier Fälle (Zeilen) wird also in einer Zahl erfasst, die die Informationen zum Vergleich je zweier Fälle (Zeilen) in einem Kennwert vereint. Für die konkrete rechnerische Vorgehensweise gibt es unterschiedlichste Varianten. Sie hängen davon ab, aus welchen Variablenarten der Datensatz besteht.
Ein einzelner Distanzwertwert beschreibt jeweils nur die Beziehung zweier Zeilen zueinander. Um die ganze Abundanztabelle auszuwerten, wird der Vorgang so oft wiederholt, bis für alle Fallvergleiche Werte vorliegen. Diese werden in einer neuen Tabelle, der Distanzmatrix (vgl. u. 2.7.) vermerkt. Verwendet man multivariate Methoden die mit Distanzmaßen arbeiten, ist es für ein wissenschaftlich sinnvolles Vorgehen von grundlegender Bedeutung, ein den Daten angemessenes Distanzmaß zu verwenden (s. u. 2.4.). Da in der Ökologie über viele Jahrzehnte intensiv zu Distanzmaßen für verschiedenste Datenarten und deren Eigenschaften geforscht wurde, kann man sich sicher sein, dass die dort entwickelten Maße ein effektives Mittel zum besagten Zweck sind. Bei der Wahl des Distanzmaßes muss man also nur auf dessen Anforderungen an die Variablenart und seine Art zu messen achten, sonst kann eine weitere Auswertung irregeleitet sein.
Die Chorddistanz ist ein sinnvolles Distanzmaß für Abundanzen (Typenvergesellschaftungstabellen).
2.2. Beispiel
Wie soll das gehen, die “Distanz” zweier Fälle (Zeilen) messen? Ein Beispiel: man stelle sich eine Tabelle mit Fällen in den Zeilen und zwei Spalten für die Typenhäufigkeiten vor. Jetzt behandelt man die beiden Spalten einfach wie die Koordinatenspalten x und y. Alle Fälle lassen sich jetzt als Punkte in einem X-Y-Streudiagramm abbilden. Die Fälle werden also als Punkte im einem Raum abgebildet, der durch die Spalten definiert wird. Je mehr Spalten, desto mehr Dimensionen hat der Raum. Eine multivariate Information zu einem Fall wird als multidimensionale Koordinate aufgefasst. Je näher sich die Punkte in diesem Koordinatenraum liegen, desto ähnlicher sind ihre Koordinaten bzw. desto ähnlicher sind die Zusammensetzungen der entsprechenden Fälle. Im Prinzip kann man sich die Funktionsweise von Distanzmaßen so vorstellen. In dem Punktebeispiel lässt sich die Ähnlichkeit der Koordinaten zweier Punkte daran erkennen, wie weit die Punkte im Diagramm auseinander liegen. Haben zwei Fälle die gleiche Zusammensetzung, dann stehen in den entsprechenden beiden Zeilen die gleichen Koordinaten. Die Punkte liegen dann aufeinander und ihr Abstand – ihre Distanz – beträgt Null. Die Ähnlichkeit der Zeilen wird in diesem Beispiel also indirekt (!) über die Unähnlichkeit der Zeilenkoordinaten – ihre Distanz im Diagramm – gemessen. Für die zugrunde liegenden Berechnungen (hier die euklidische Distanz; s. u. 3.) ist es egal, ob die Tabelle zwei oder zweiunddreissig Spalten besitzt, das Prinzip ist dasselbe: je näher sich zwei Punkte im multidimensionalen Raum der Variablen sind, desto ähnlicher sind sie sich bzw. desto geringer ist ihre Distanz.
An dem Beispiel erkennt man, dass sich die Ähnlichkeit zweier Zeilen bei vielen Datenarten – etwa metrischen Variablen wie die Koordinaten im Beispiel – nur indirekt über die Unähnlichkeit erfassen lässt. Bei vielen multivariaten Datensätzen und insbesondere bei Typenvergesellschaftungstabellen führt aber diese naive Variante der Distanzberechnung (die sog. Euklidische Distanz) zu Verzerrungen, die schlechte bis falsche Ergebnisse hervorbringen können. Mit einer Auswertung auf der Basis der Chorddistanz vermeidet man diese Fehlerquellen.
2.3. Distanz- und Ähnlichkeitsmaß
Bei einigen Datenarten, so auch bei Abundanzen, gibt es Möglichkeiten den Grad der Übereinstimmung zweier Zeilen, also ihre Ähnlichkeit, direkt zu messen. In der Ökologie wurden mehrere solcher sog. Ähnlichkeitsmaße entwickelt. Um damit aber Methoden benutzen zu können, die Distanzangaben benötigen, kann man das Ähnlichkeitsmaß in ein Distanzmaß umrechnen.
Für die Umrechnung der Ähnlichkeit in die Distanz (Unähnlichkeit) wird zumeist das Ähnlichkeitsmaß so standardisiert, dass es nur Werte zwischen Null und Eins annehmen kann. Null entspricht bei einem Ähnlichkeitsmaß völliger Unähnlichkeit und Eins entspricht völliger Übereinstimmung der Zeilen. Das Distanzmaß wird nun aus der Differenz von Eins und dem Ähnlichkeitsmaß gebildet. Das Distanzmaß kürzt man mit D ab, das Ähnlichkeitsmaß mit Ä (im Englischen S für “similarity”). Die Distanz wird dann berechnet als D = 1 – Ä. Bei grösstmöglicher Ähnlichkeit ist Ä gleich 1 und es ergibt sich für D = 1- Ä die Formel D = 1 – 1 = 0. Die Distanz bzw. die Unähnlichkeit ist 0. Im entgegengesetzten Fall bei völliger Unähnlichkeit ist Ä = 0 und es ergibt sich D = 1 – 0 = 1. Distanzmaße, die so aus Ähnlichkeitsmaßen abgeleitet wurden schwanken also zwischen 0 und 1. Bei 0 beträgt die Distanz zweier Fälle Null und die beiden Zeilen stimmen völlig überein. Bei 1 ist die Distanz maximal und die beiden Fälle haben nichts gemeinsam. Viele Ähnlichkeitsmaße lassen sich so in Distanzen umrechnen.
Ohne hier auf die Details einzugehen muss leider festgehalten werden, dass viele dieser aus Ähnlichkeitsmaßen abgeleiteten Distanzmaße einige bestimmte, wünschenswerte rechnerische Eigenschaften nicht besitzen. Aus diesem Grund wurde unter anderem die Chorddistanz entwickelt. Bei der Chorddistanz beträgt der Minimalwert bei völliger Übereinstimmung 0. Der Maximalwert bei totaler Unähnlichkeit ist aber nicht 1, sondern 1,4142 (die Wurzel aus 2). Warum dies so ist, wird im Abschnitt zur Geometrie erläutert (s. u. 5.).
2.4. Variablenart und Distanzmaß
Oftmals liegt eine Datenbank vor, die vollständig aus Variablen nur einer Art besteht. Es können etwa nur metrische Variablen sein, die mehrere Abmessungen von Objekten beinhalten. In einem anderen Fall besteht die Datentabelle nur aus ordinalen Variablen wie etwa den Bewertungen von stilistischen Aspekten prähistorischer Kunstgegenstände. Daneben gibt es Situationen, in denen man für eine Reihe von Merkmalen nur abgefragt hat, ob bestimmte Merkmalsausprägungen anwesend oder abwesend sind, sog. binäre Variablen.
Hier geht es um Datensätze der Art “Typenvergesellschaftungstabelle” (Abundanztabelle). Bei Typenvergesellschaftungstabellen könnte das Merkmal beispielsweise die Verzierung und die Ausprägungen bestimmte Verzierungsvarianten sein. Und dann kann es natürlich noch Datentabellen geben, die verschiedene Variablenarten enthalten. Für jede dieser Varianten gibt es unterschiedliche Distanzmaße zur Komprimierung der multivariaten Information. Das ist deshalb so, weil für die jeweiligen Variablenarten jeweils nur bestimmte Rechenwege erlaubt bzw. sinnvoll sind. Für metrische Variablen verwendet man andere Distanzmaße als etwa für binäre Variablen. Für ordinale Variablen – also die Information “mehr oder weniger” bzw. “besser oder schlechter” – sind wiederum andere Distanzmaße zu verwenden. Für die meisten Variablenarten gibt es wie gesagt mehrere sinnvolle Distanzmaße. Jedes dieser Maße wurde im Hinblick auf eine bestimmte, wiederholt auftretende, Problemsituationen entwickelt und misst deshalb Distanz auf andere Weise.
Die Wahl des Distanzmaßes ist in erster Linie eine archäologische Entscheidung über die Angemessenheit einer bestimmten “Messvorliebe” des Maßes für die wissenschaftliche Fragestellung. Erst an zweiter Stelle steht die Entscheidung für das jeweilige statistische Verfahren – und dabei geht es eigentlich nur um die technisch korrekte Einengung der in Frage kommenden Maße. Die Chorddistanz ist ein Distantmaß für Abundanztabellen (Typenvergesellschaftungstabellen), das seine (Un-)Ähnlichkeitsmessung auf dem Vergleich der Zeilenprozente gründet. Unterschiede der Zeilensummen gehen nicht in die Messung ein.
2.5. Abundanztabelle
Bei einer Typenvergesellschaftungstabelle, einer sog. Abundanztabelle, sind in den Spalten die absoluten Häufigkeiten bzw. Anzahlen bestimmter Ausprägungen eines Merkmal vermerkt. Jede Spalte erfasst dabei, wie oft eine bestimmte Ausprägung des Merkmals, etwa ein Typ, bei den verschiedenen Fällen vorkommt. Eine Abundanztabelle enthält also Nullen oder ganze positive Zahlen. Es handelt sich um ein “Zahlenfeld”, eine Anordnung von Zahlen. In der Mathematik werden sie als Matrix bezeichnet.
Für Interessierte sei hier angemerkt, dass Matrixalgebra die rechnerische Grundlage der allermeisten modernen multivariaten Verfahren bildet. In R kann man quasi “von Hand” Matrixalgebra rechnen und auf diese Weise genau die Rechenwege der Verfahren nachvollziehen. So lässt sich ein genaues Verständnis der Funktionsweise statistischer Methoden erlernen – zumindest nach meinen Erfahrungen. Doch zurück zur Chorddistanz…
Wenn man etwa als Untersuchungsobjekte (Zeilen) einer Abundanztabelle Gräber erfasst, so könnte das Merkmal für die Spalten beispielsweise das Grabbeigabenspektrum sein. Als Ausprägungen des Merkmals “Beigabe”, also als Spalten, kämen etwa in Frage: Keramik, Schmuck, Waffen und Werkzeuge. Jede Ausprägung entspricht einer Spalte. In den Zellen der Tabelle steht dann, wie oft diese Ausprägung bei dem jeweiligen Fall (Zeile) auftritt. Dieses Beispiel zeigt, dass das Nominalmerkmal für die Spalten einer Abundanztabelle durchaus ein abstraktes, aber wissenschaftlich gut begründetes Phänomen sein kann. In der Ökologie ist es häufig das Merkmal Tierarten- bzw. Pflanzenartenspektrum, wobei in den Spalten die Anzahlen jeweils einer Art in den Untersuchungsarealen (Zeilen) stehen. Man sieht, Ökologie und Archäologie verwenden völlig gleichartig strukturierte Informationen.
Eine nützliche archäologische Abundanztabelle zeichnet sich dadurch aus, dass das Nominalmerkmal für die Spalten ein Phänomen ist, das sinnvoll anhand der Abundanzen erfasst werden kann. Die definitorische Formulierung dessen, was als Phänomen wie mit welchen Ausprägungen anhand einer Abundanztabelle beschrieben werden kann, ist Aufgabe der Theorie der Archäologie und nicht der statistischen Methode. Beispiele für sinnvolle Abundanzen sind etwa: die Häufigkeiten unterschiedlicher Mikrolithentypen an mesolithischen Fundstellen, die Anzahlen verschiedener Gefäßformen in neolithischen Gruben oder die pro Schicht aufgefundenen Amphorentypen.
2.6. Symmetrie eines Distanzmaßes
Wie erwähnt wird eine Distanz zwischen zwei Fällen (Zeilen) durch den Vergleich jeweils einer Zelle der einen und einer Zelle der anderen Zeile berechnet. Am Ende aller Zellenvergleiche steht die Zusammenfassung aller Einzelvergleiche im Distanzmaß. Bei Abundanzen kann es vorkommen, dass der eine Fall in einer Zelle den Wert Null aufweist, während beim anderen diese Ausprägung vorkommt. D. h., es gibt bei dem einem Fall einmal die Merkmalsausprägung der entsprechenden Spalte nicht. Bei archäologischen Abundanzen kommt dies sogar häufig vor. Nicht selten ist es bei archäologischen Phänomenen auch, dass eine Merkmalsausprägung bei beiden Fällen nicht auftritt. Die “Gemeinsamkeit” der Fälle besteht dann bei der Ausprägung dieser Spalte darin, dass die Ausprägung bei beiden abwesend ist. Abhängig davon, welche Fragestellung man hat, muss man sich nun entscheiden.
Soll das Distanzmaß Abwesenheit genauso wie Anwesenheit bewerten? Oder soll es die Abwesenheit unberücksichtigt lassen. Bei den allermeisten archäologischen Fragestellungen wird man aus theoretischen Gründen die zweite Variante bevorzugen. Dass etwa zwei Befunde sich deswegen besonders ähnlich sein sollen, weil viele Ausprägungen (Typen) bei beiden nicht vorkommen ist in den wenigsten Fällen eine einleuchtende Annahme. Wenn man etwa die Gefäßformen in neolithischen Befunden erfasst, würde die Messung einer gemeinsamen Abwesenheit als Ähnlichkeit dazu führen, dass sich altneolithische und endneolithische Befunde besonders ähnlich sind, weil beide sehr viele Gefäßformen gemeinsam nicht (!) aufweisen.
Diese Art des Vorgehens bedeutet, Ähnlichkeit negativ zu definieren. Mir fällt nur eine Situation ein, bei der ein solches Vorgehen sinnvoll sein kann. Wenn man a priori einen bestimmten Kanon von Ausprägungen annehmen muss, die bei allen Fällen mehr oder weniger häufig auftreten, ist eine negativ definierte Ähnlichkeit sinnvoll. In diesem Spezialfall bestünde dann die Ähnlichkeit zweier Fälle darin, dass sie beide diesen Kanon verletzen.
Tritt eine Merkmalsausprägung nicht auf, so enthält die Abundanztabelle an dieser Stelle die Information “Abwesenheit” bzw. Absenz. Die Interpretation von Absenzen ist in der Archäologie genauso problematisch wie in der Ökologie (vgl. Legendre/Legendre 1998, 253). Bei Abundanzmatrizen bedeutet eine Null – also Absenz einer Ausprägung – die Abwesenheit von Information. Eine solche Null ist nicht das gleiche wie etwa eine Null in einer Datentabelle mit Bodenchemiewerten, bei denen beispielsweise Phosphatgehalt Null auch wirklich bedeutet, dass es kein Bodenphosphat gibt (im Rahmen der Messgenauigkeit natürlich). Bei Typen kann diese “abwesende” Information viele Gründe haben. Wurde die entsprechende Typvariante nur nicht gefunden? War sie zufällig bei dem untersuchten Fall gerade einmal nicht vorhanden? Tritt sie nur bei Fällen einer bestimmten Phase auf oder nur bei Fällen einer bestimmten Region? Spätestens wenn diese Aspekte die Fragestellung tangieren, etwa bei der Erforschung einer Relativchronologie oder einem Regionalvergleich, würde man sich als skeptischer Archäologe dafür entscheiden, Absenz und Präsenz bei der Distanzmessung nicht auf gleiche Weise zu berücksichtigen.
Distanzmaße, die die Absenz einer Merkmalsausprägung anders als Präsenzen bewerten, und somit (Un-)Ähnlichkeit anders messen, werden als asymmetrische Maße bezeichnet. Solche, die Absenzen auf die gleiche Weise wie Präsenzen bewerten, heissen symmetrische Maße. Die Chorddistanz ist ein asymmetrisches Distanzmaß. Sie bewertet Absenzen anders als Präsenzen. Die Distanzberechnung ist wie gesagt ein zusammenfassender Schritt. Benutzt man ein symmetrisches Maß, unterstellt man, dass Präsenz und Absenz gleich bewertet werden dürfen, weil sie aus den gleichen Kausalitätszusammenhängen hervor gehen. Die obigen Erwägungen zeigen aber, dass dem in der Archäologie in der Regel nicht so ist. Für die allermeisten archäologischen Fragestellungen muss daher Präsenz anders bewertet werden als Absenz. Wenn beispielsweise mögliche Ursachen der Absenz die Fragestellung (Relativchronologie oder Regionalstudie) tangieren, sollte man unbedingt ein asymmetrisches Distanzmaß verwenden (a. a. O. , 254). Bei der Verwendung des Begriffes Symmetrie ist einer möglichen Verwechslung vorzubeugen. Man verwechsle nicht das Symmetriegebot für ein Distanzmaß mit der (a-)symmetrischen Bewertung von gemeinsamen Absenzen! Das Symmetriegebot besagt, die Distanz von Zeile a zu Zeile b muss der Distanz von Zeile b zu Zeile a entsprechen. Die Chorddistanz erfüllt dieses Gebot. Das Adjektiv asymmetrisch bezieht sich ausschliesslich (!) auf die unterschiedliche (asymmtrische) Bewertung von Präsenzen und Absenzen.
Die euklidische Distanz, die leider immer noch oft – weil Standardeinstellung (!) vieler Programme – zur Clusteranalyse von Abundanzen verwendet wird, ist dagegen ein symmetrisches Maß. D. h., sie bewertet einen Unterschied zwischen 4 und 2 genauso wie einen Unterschied zwischen 2 und 0. Null bedeutet im Fall einer Abundanztabelle wie gesagt nicht eine Messung des Wertes 0 sondern die Abwesenheit der Ausprägung. Alle positiven Zelleinträge repräsentieren gemeinsam Präsenz in unterschiedlicher Ausprägung. Der Wert Null repräsentiert Absenz. Beide Male geht bei dem gerade beschriebenen Zahlenbeispiel eine Differenz von 2 in die Berechnung der Distanz zweier Fälle ein. Beim ersten Beispiel wurde aber die Unterschiedlichkeit einer Information erfasst. Beim zweiten besteht der Unterschied zwischen vorhandener und abwesender Information. Die Eukliddistanz beachtet diesen Unterschied nicht. Deshalb ist sie für die distanzbasierte archäologische Analyse von Abundanztabellen nicht geeignet (vgl .u. das Beispiel bei 3.).
2.7. Distanzmatrix
Hat man sich für ein zu den verwendeten Daten passendes Distanzmaß entschieden, dann wird die Messung für alle möglichen Paarungen zweier Fälle (Zeilen der Abundanztabelle) wiederholt. Aus jedem Vergleich zweier Fälle (Zeilen) ergibt sich somit ein Distanzwert. Dieser wird in eine neue Tabelle, die sog. Distanztabelle oder Distanzmatrix, geschrieben. Zeilen- und (!) Spaltenanzahl der Distanzmatrix entsprechen jeweils der Anzahl der Zeilen in der Abundanztabelle. Jeder Fall erscheint einmal als Zeile und einmal als Spalte der Distanzmatrix. Die Reihenfolge der Fälle ist bei den Zeilen und den Spalten der Distanzmatrix gleich. In einer Zelle der Matrix steht nun die Distanz zwischen dem “Zeilenfall” und dem “Spaltenfall”. In der ersten Zeile steht etwa in der dritten Zelle die Ähnlichkeit zwischen dem ersten Fall (erste Zeile der Abundanztabelle = erste Zeile der Distanzmatrix) und dem dritten Fall (dritte Zeile der Abundanztabelle = dritte Spalte der Distanzmatrix). Die Zelle in der fünften Spalte der vierten Zeile enthält die Ähnlichkeit zwischen Fall vier und Fall fünf usw. Auf der Diagonalen der Tabelle steht die Distanz eines Falles zu sich selbst, also Null.
Die Distanzmatrix ist eine sog. symmetrische Matrix. In den Zellen rechts oberhalb der Diagonalen steht genau die gleiche Information wie links unterhalb der Diagonalen. Die Distanz von Fall drei zu Fall sieben (Zelle in der dritten Zeile, siebte Spalte) ist ja genau die gleiche wie die Distanz von Fall sieben zu Fall drei (Zelle in der siebten Zeile, dritte Spalte). Man kann also eine Distanzmatrix ohne Informationsverlust darstellen, wenn man nach der Berechnung nur die untere linke oder die obere rechte dreieeckige Matrixhälfte beibehält. Wenn solche Matrizen in der “überflüssigen” Dreieckshälfte Nullen enthalten, dann heissen sie Dreiecksmatrizen.
Die meisten kennen ein typisches Beispiel für eine Distanzmatrix, nämlich eine Tabelle mit den geographischen Distanzen zwischen Städten. Am linken Tabellenrand stehen bei den Zeilen Städtenamen und am oberen Tabellenrand stehen ebenfalls Städtenamen; in den Zellen stehen die geographischen Entfernungen zwischen den Städten, man kann auch sagen, ihre geographischen Distanzen. Das hier verknüpfte Beispiel zeigt die Distanzen zwischen irischen Städten. In einer Zelle der Zeile Sligo und der Spalte Dublin steht die Entfernung zwischen beiden, nämlich 213 km. Da entlang der Diagonale Nullen und rechts oberhalb der Diagonalen spiegelbildlich die gleichen Werte wie links unterhalb der Diagonalen stehen würden, hat man diesen Teil beim Beispiel einfach weggelassen. Die Information einer Distanztabelle ist also bereits vollständig in einer der zwei dreieckigen Hälften der Tabelle enthalten. Es genügt völlig, nur diesen Tabellenteil darzustellen. In der Distanzmatrix einer Abundanztabelle steht natürlich eine auf andere Weise gemessene Distanz als beim Städtebeispiel.
Eine Distanzmatrix ist das Endergebnis der Distanzberechnung und der Ausgangspunkt für verschiedene multivariate (geostatistische) Methoden. Mit der Berechnung der Chorddistanzen für eine Abundanztabelle verfügt man über eine sinnvolle Ausgangsbasis, um nach der Anwendung solcher Verfahren verzerrungsfreie bzw. fehlerfreie Ergebnisse zu erhalten.
3. Euklidische Distanz und Abundanzen
Die wichtigste und zugleich mit unserem Alltagsverständnis am besten nachvollziehbare Distanz ist der räumliche Abstand in der realen Welt. Dieser reale Raum ist – zumindest auf der Erde und ohne Verzerrungen durch starke Gravitationsfelder – ein sog. euklidischer Raum. Abstände in einem solchen Raum erfüllen bestimmte Eigenschaften und werden deshalb auch als euklidische Distanzen bezeichnet. So ist etwa der Abstand zwischen der eigenen Nasenspitze und dem Ohrläppchen eine euklidische Distanz. Die Berechnung der euklidischen Distanz haben wir alle in der 7. oder 8. Klasse als Satz des Pythagoras gelernt. Die Distanz zwischen zwei Punkten ist die Wurzel aus der Summe aller quadrierten Koordinatendifferenzen. In einer zweidimensionalen Fläche mit X- und Y-Achse berechnet sich der “Pythagoras” zu: (“Koordinatenunterschied zwischen Punkt A und B auf der X-Achse”) zum Quadrat plus (“Koordinatenunterschied zwischen Punkt A und B auf der Y-Achse”) zum Quadrat gleich Quadratesumme. Die Wurzel aus dieser Quadratesumme ist der Abstand der Punkte A und B.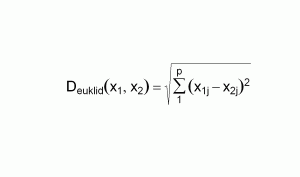
Zusammengefasst: die Wurzel aus der Summe der quadrierten Koordinatendifferenzen ist die Eukliddistanz. Als statistische Formel sieht das dann so aus. Die Abundanztabelle hat p Spalten. Es ist x [1j] die Häufigkeit der Ausprägung j in der ersten der beiden verglichenen Zeilen und x [2j] die Häufigkeit der Ausprägung j in der zweiten der beiden verglichenen Zeilen. Das grosse Sigma mit dem p obendrauf besagt, summiere alle Elemente mit einem variablen Subskript – hier also die x-e – für alle Spalten auf. Es wird also die Summe gebildet aus den Quadraten der Differenzen der beiden Häufigkeiten.
Der Grund für die Beliebtheit der Eukliddistanz sind ihre rechnerischen Eigenschaften, die im Prinzip alle Rechenarten erlauben. Achtung: jetzt besteht Verwirrungsgefahr! Man beachte den Unterschied zwischen DER euklidischen Distanz, der Eukliddistanz, und Distanzen mit euklidischen Eigenschaften. Distanzmaße die folgende Eigenschaften besitzen, werden als Distanzen mit euklidischen Eigenschaften, oder besser als metrische Distanzmaße bezeichnet. Für die folgende Auflistung wird aus Verständnisgründen statt Merkmalseigenschaften der oben im Beispiel benutzte Begriff “Koordinaten” verwendet, weil er beim bildlichen Vorstellen hilfreich ist. Die angesprochenen Distanzmaßeigenschaften lauten:
- Der Abstand zwischen einem Punkt A und einem Punkt B mit exakt gleichen Koordinaten, kurz AB, ist gleich Null.
- Der Abstand von A zu einem B mit ungleichen Koordinaten ist grösser als Null.
- Der Abstand von A zu B entspricht dem Abstand von B zu A (DIES ist das oben unter 2.6. angesprochene Symmetriegebot für Distanzmaße).
- Wenn A, B und C verschiedene Positionen besitzen, ist der Abstand AB + BC grösser oder gleich dem Abstand AC. Der Abstand ist gleich der Summe, wenn A, B und C auf einer Linie liegen. Bei metrischen Distanzmaßen kann man mit den Strecken (Distanzen) AB, BC und CD ein Dreieck bilden. Bei nicht metrischen ist eine der Distanzen “zu lang” oder “zu kurz”. Nichtmetrische Distanzmaße verhalten sich bei multivariaten Methoden, die mit einem Matrixalgebraverfahren namens Eigenwertzerlegung arbeiten, unschön. Sie erzeugen negative Eigenwerte. Dadurch werden sie für wichtige Verfahren unbrauchbar.
Diese Eigenschaften sind wichtig, um bestimmte Rechenverfahren zur Auswertung der Distanztabelle anwenden zu dürfen(!). Wenn man sich nicht sicher ist, welche Ansprüche die Rechenwege eines Verfahrens an das Distanzmaß stellen, ist man bei der Wahl eines metrischen Distanzmaßes auf der sicheren Seite. Es sei aus Verständnisgründen nochmals wiederholt, dass DIE euklidische Distanz und eine Distanz mit euklidischen (metrischen) Eigenschaften NICHT das Gleiche sind. Sie können aber mit den gleichen Verfahren ausgewertet werden. Das macht metrische Distanzmaße, also Maße mit euklidischen Eigenschaften, zu den besten Verfahren der (Un-)Ähnlichkeitsmessung. Die Chorddistanz ist ein metrisches Distanzmaß und besitzt diese euklidischen Eigenschaften.
Warum ist denn jetzt diese einfach verständliche Euklid-Distanz nicht geeignet für Abundanzen? Nun, der wichtigste Aspekt, die Notwendigkeit der asymmetrischen Bewertung von Präsenzen und Absenzen wurde bereits oben diskutiert (s. o. 2.6.). Ein weiterer ebenso problematischer Punkt ist die Abhängigkeit der Eukliddistanz von den absoluten Anzahlen, also den absoluten Häufigkeiten der Typenausprägungen (Orloci 1967, 195f.; vgl. Kindt/Coe 2005, 126). Wenn beispielsweise bei zwei Fällen die Ausprägungen in genau den gleichen Anteilen vorliegen, der eine aber doppelt soviele Funde, wie der andere enthält, dann verzeichnet die Eukliddistanz einen deutlichen Unterschied, obwohl die beiden Fälle völlig gleich zusammengesetzt sind. Sobald also bei archäologischen Abundanzen auch nur kleinere absolute Häufigkeitsunterschiede eine Rolle spielen, dann erzeugt eine Distanzmessung der Zusammensetzung mit der Eukliddistanz falsche Informationen. Ebenso problematisch ist aber der Effekt, wenn zwei Fälle (Zeilen) in vielen Zellen gemeinsam Nullen aufweisen. Wie man anhand des Pythagoras leicht nachvollziehen kann, wird diese Situation als ein Abstand von Null in dieser Dimension, also als vollständige Übereinstimmung bei diesem Typ gemessen. Je mehr Nullen zwei Zeilen gemeinsam haben, desto “ähnlicher” werden sie sich durch dieses symmetrische Bewerten von Absenz und Präsenz(vgl. o. 2.6.). Dieser problematische Effekt gemeinsamer Nullen bei Zeilenpaaren einer Abundanztabelle erhielt in der Ökologie die Bezeichnung Doppel-Null-Problem (“Double-zero problem”; Legendre/Legendre 1998, 253). 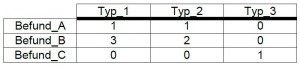
Das folgende Zahlenbeispiel verdeutlicht die mangelnde Eignung der Eukliddistanz. Ein intuitives und zugleich archäologisch sinnvolles Distanzmaß muss bei der nebenstehenden Abundanztabelle ausdrücken, dass sich Befund A und Befund B deutlich ähnlicher sind als Befund A und C bzw. B und C, denn letzterer hat keinen einzigen Typen mit A oder B gemeinsam. Und nun das böse Erwachen mit der Eukliddistanz:
Befund A ist bei dieser Art, zu messen, dem Befund C ähnlicher als dem Befund B, 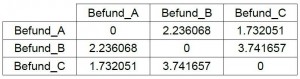 obwohl er mit B alle Typen gemeinsam hat, während er mit C keinen gemeinsam hat. DAS ist der Effekt des symmetrischen Distanzmaßes.
obwohl er mit B alle Typen gemeinsam hat, während er mit C keinen gemeinsam hat. DAS ist der Effekt des symmetrischen Distanzmaßes.
Dieses Problem bei der Anwendung der Eukliddistanz auf Abundanzen ist schon lange bekannt und wurde 1978 von Orloci als “Arten-Abundanz-Paradox” (“species abundance paradox”; ders. 1978, 46) bezeichnet. Es ist das auch in anderen Lehrbüchern (z. B. Legendre/Legendre 1998, 278) verwendete Standardbeispiel für die mangelnde Eignung der Eukliddistanz zur Messung von Abundanzunähnlichkeiten.
Im Vorgriff wird an dieser Stelle schon einmal die Chorddistanz berechnet, um den Vorteil des asymmetrischen Distanzmaßes Chord gegenüber dem symmetrischen Euklid zu demonstrieren.
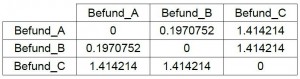 Jetzt spiegeln sich die Beziehungen plausibel wider. Befund A ist Befund B ziemlich ähnlich (0.197) und beide sind von Befund C durch die maximal mögliche Chorddistanz von 1.4142 getrennt, denn sie haben ja nichts gemeinsam.
Jetzt spiegeln sich die Beziehungen plausibel wider. Befund A ist Befund B ziemlich ähnlich (0.197) und beide sind von Befund C durch die maximal mögliche Chorddistanz von 1.4142 getrennt, denn sie haben ja nichts gemeinsam.
Zur Erinnerung, bildet man die multivariaten Informationen der Fälle (Zeilen) eines Datensatzes mit einem Distanzmaß ab, so werden alle Informationen zu jeweils zwei Fällen in einer Zahl erfasst und es gehen alle Details zur Ursache der Distanz verloren. Man behält einzig die jeweils paarweisen Unterschiede der Fälle ohne an diesen Zahlen ablesen zu können, welche Variablen zur jeweiligen Distanz wie beigetragen haben. Aufgrund der extremen Informationszusammenfassung, die das Auswerten von Distanzmaßen darstellt, ist grosse Sorgfalt bei der Wahl des für die Daten geeigneten Distanzmaßes erforderlich. Die Chorddistanz kann die Distanzen zwischen Zeilen von Typenvergesellschaftungstabellen (Abundanzmatrizen) archäologisch angemessen widergeben.
Wenn man statt dessen Abundanztabellen auf der Basis eines naiven Maßes wie der Eukliddistanz auswertet, wird sicher jede Clusteranalyse und jede nichtmetrisch multidimensionale Skalierung ein Ergebnis liefern. Die Methoden tun, was man ihnen sagt. Sie können ja nicht mitdenken. Was aber archäologisch vom Endergebnis zu halten ist, kann man sich anhand dieses Beispiels ausmalen.
4. Berechnung der Chorddistanz
Die Idee zur Chorddistanz basiert darauf, die Zeilen einer Tabelle als Vektoren darzustellen. Ein detailliertes Beispiel zum Verständnis wird im nächsten Abschnitt präsentiert. Wer sich bei mathematischen Begriffen etwas unwohl fühlt, möchte möglicherweise dessen Lektüre vorziehen (s. u. 5.). Von der Idee her entspricht der Ansatz dem oben unter 2.2. vorgestellten Koordinatenbeispiel. Der Vektor einer Zeile ist der Pfeil vom Ursprung des Koordinatensystems (die Spalten sind die Koordinaten) zu dem Punkt, der durch Benutzung der Zeileneinträge als Koordinate entsteht. 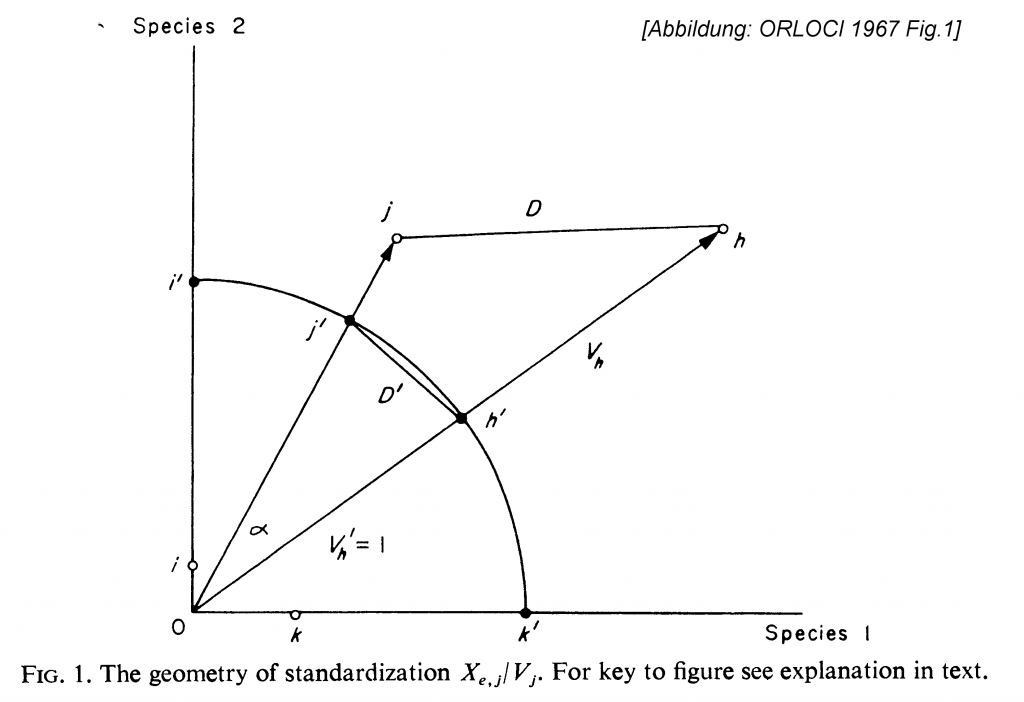
Orlocis (1967) Idee war es nun, dass ähnliche zusammengesetzten Zeilen zu Zeilenvektoren führen, die annähernd in die gleiche Richtung zeigen. Mit den einfachen Vektoren kann man aber nicht sinnvoll die Distanz messen, denn das entspräche der Eukliddistanz. Der Vektor wird ja umso länger, je grösser die Zeilensumme der Abundanztabellenzeile ausfällt. Auch wenn zwei Vektoren in die exakt gleiche Richtung zeigen (also identisch zusammengesetzte Fälle vorliegen) wäre der Endpunkt des einen deutlich von Endpunkt des anderen entfernt. Bei der Verwendung der Eukliddistanz ergäbe sich dadurch eine Distanz, die nicht gerechtfertigt ist.
Um unterschiedlich stark besetzte Zeilen zu vergleichen bedarf es also einer Normierung. An dieser Stelle hatte Orloci die zündende Idee. Wenn man die Vektoren auf die Länge 1 standardisiert, also alle Zelleneinträge durch die Länge des Vektors teilt, dann lässt sich der “Richtungsunterschied” zweier Vektoren auch anders erfassen. Das Teilen der einzelnen Elemente (Koordinaten) eines Vektors durch dessen Länge wird auch als Normalisierung bezeichnet. Nach der Normalisierung der Vektoren liegen alle Vektorenendpunkte auf einem Einheitskreis bzw. einer Einheitskugel. Die Länge der Linie zwischen den neuen Vektorenendpunkten ist nun ein metrischer (!) Ausdruck der Richtungsgleichheit zwischen zwei Vektoren. Es ist die Sehne (Englisch “chord”) des Kreises (bzw. der Kugel) über die Vektorenendpunkte. Deren Länge lässt sich mit dem Pythagoras berechnen. Durch den Schritt der Normalisierung spielt allerdings die Information zur Zeilensumme und damit auch zu den absoluten Zahlenunterschieden der beiden Zeilenvektoren bei der Distanzmessung keine Rolle mehr. Andrerseits werden so Zeilen mit sehr verschiedenen Zeilensummen gut vergleichbar. Auf diese Weise hat man die bekannten Probleme umgangen, die sich aus der euklidischen Distanz ergeben und verfügt trotzdem über ein metrisches Distanzmaß.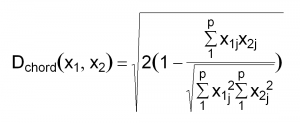
Orloci folgte konsequent seiner geomtrischen Herleitung der Distanzberechnung und präsentierte dieses von ihm als “Standarddistanz” bezeichnete Maß mit einer entsprechenden, geometrische Terme (Formelteile) nutzenden, Formel (Formel bei Orloci 1967, 196). Die Formel liest sich folgendermaßen. Die x1j bzw. x2j sind die Zelleneinträge in der j-ten Spalte der Zeile x1 bzw. x2. Das Subskript j erreicht maximal den Wert p, der der Anzahl der Spalten entspricht. Ein grosses Sigma bedeutet, bilde die Summe aller Elemente, die ein variables Subskript aufweisen. Hier ist es das Subskript j. Die Summe soll alle Elemente mit Subskripten von j=1 bis zu j=p enthalten.
Über dem Bruchstrich steht also die Summe aus allen Produkten sich in der Spalte entsprechender Zellen – das Mal-Zeichen wird in solchen Formeln grundsätzlich weggelassen. Unter dem Bruchstrich werden die x1j bzw. x2j quadriert und dann diese Quadrate für jede Zeile getrennt aufsummiert. Danach wird das Produkt aus diesen beiden Summen gebildetund daraus wieder die Wurzel gezogen. 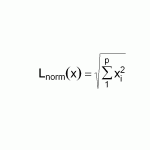
Der Term unter dem Bruchstrich kommt einem irgendwie bekannt vor, nicht? Genau, die Wurzel aus einer der Summen entspricht der mit dem Pythagoras berechneten Länge eines Zeilenvektors, der sog. Norm. Was sagt die Formel hier? Das xi ist der i-te Zelleneintrag einer Zeile. Also quadriere jeden Zelleneintrag, bilde die Summe aller Quadrate von der ersten bis zur letzten Spalte und ziehe dann die Wurzel.
Unter dem Bruchstrich der Chorddistanzformel in ihrer “geometrischen Variante” steht also das Produkt aus den Längen der beiden Zeilenvektoren (vgl. Wickens 1995, 13). Über dem Bruchstrich steht ein Term, der dem einen oder anderen von der Berechnung einer Korrelation (der Beziehung zweier metrischer Variablen) bekannt ist. Dieser Ausdruck heisst in der Matrixalgebra Skalarprodukt oder inneres Produkt der beiden Vektoren und besitzt tatsächlich eine Beziehung zur Gemeinsamkeit der zwei Vektoren (ibid).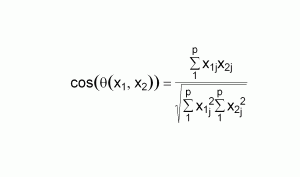
Der ganze Bruch drückt also eine Gemeinsamkeit geteilt durch eine Gesamtheit aus. Bei metrischen Variablen entspricht er tatsächlich dem mit r bezeichneten Korrelationskoeffizienten nach Pearson (Wickens 1995, 19; Formel ibid (2.18)). In der Matrialgebra entspricht der Bruch dem Cosinus des Winkels zwischen beiden Vektoren. Den Cosinus kann man auch so verstehen, dass er den Anteil angibt, zu dem die Länge des einen Vektors der Länge des anderen Vektors entspricht. In der Welt der Variablen bedeutet, es ist der Grad in dem sich die Werte bei zwei Variablen entsprechen, also ihre Korrelation.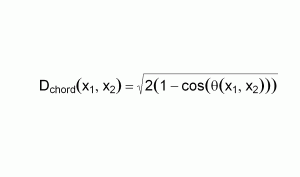
Für das Verständnis der Funktionsweise ist eine weitere Formelvariante der Chorddistanz interessant. Ersetzt man den Bruch in der Formel der Chorddistanz mit dem Cosinus, so lässt sich die Formel auch ohne Bruch schreiben und vereinfacht sich zu der Wurzel einer verdoppelten Differenz (Formel bei Orloci 1967, 196). Die Chorddistanz wird so einfach als Funktion des Cosinus des Winkels zwischen den beiden Vektoren.
Bereits Orloci (a. a. O., 196) hatte schon eine weitere Formelvariante vorgestellt, die stärker herausstellte, dass seine “Standarddistanz” euklidische Eigenschaften besitzt und deshalb ein metrisches Distanzmaß ist.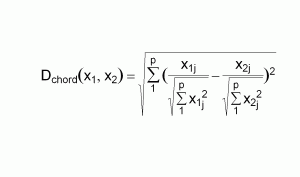
Bei dieser Variante werden die Differenzen zwischen den bereits normierten Zellenwerten mit dem Pythagoras berechnet. Die normierten Zellenwerte sind die beiden Brüche in dieser Formelvariante. Legendre und Gallagher erkannten 2001, dass eine Normierung der Zellenwerte (Abundanzwert in der Zelle) in der Abundanzmatrix, die sog. vortransformierten Abundanzwerte, der Repräsentation der Abundanztabelle als Datentabelle mit metrischen Variablen entspricht. Normierung bedeutet schlicht, man teilt den Zellenwert der Abundanzmatrix durch die Länge des Zeilenvektors. Sie präsentierten daraufhin eine weitere Variante der Formel der Chorddistanz in einer Schreibweise (Formel a.a.O., 271 (1)), die das Vorhandensein der metrischen Eigenschaften noch deutlicher zum Ausdruck brachte und die Sinnhaftigkeit der Verwendung solcherart transformierter Werte in der PCA nachvollziehbar macht. Die Auswertung einer chord-transformierten Abundanzmatriz mit einer PCA zeigt im Biplot die Chorddistanzen zwischen den Matrizenzeilen.
In dieser Formel steht wieder unter den Bruchstrichen die Länge des jeweiligen Vektors und darüber der Eintrag in der j-ten Spalte der entsprechenden Zeile. Immer noch sind x1j und x2j die Werte in der j-ten Spalte der ersten bzw. der zweiten der beiden verglichenen Zeilen. Man liest also j-ter Zellenwert Zeile 1 durch Länge des ersten Zeilenvektors minus j-ter Zellenwert der Zeile 2 durch Länge des zweiten Zeilenvektors. Diese Differenz wird quadriert. Jetzt summiert man wieder alle quadrierten Differenzen von der ersten bis zur letzten Spalte auf. Dafür steht das Sigma mit dem p darüber. Und aus dieser Gesamtsumme wird die Wurzel gezogen. Die Wurzel aus quadrierten Differenzen entspricht dem Pythagoras.
Nach dieser Herleitung der Formeln und der Erläuterung der Bedeutung ihrer Elemente ist es nun an der Zeit auf die Effekte verschiedener Ausgangssituationen für die Distanzberechnung näher einzugehen. Zunächst sei angemerkt, dass eine Division keine Unterschiede in Relationen hervorrufen kann. Das bedeutet, wenn sich die Zeilenprozente der beiden verglichenen Zeilen völlig gleichen, tun sie dies auch nach der Normalisierung. Bei völlig gleich zusammengesetzten Fällen (Zeilen) wird also j-mal das gleiche von einander abgezogen. Das ergibt jeweils Null. Und Null bleibt Null, auch wenn man sie quadriert, aufsummiert und ihre Wurzel zieht. Bei Fällen mit völlig gleichen Zeilenprozenten ergibt sich wie bei einem metrischem Distanzmaß gefordert eine Distanz von Null. Haben beide Fälle (Zeilen) jedoch nichts gemeinsam, so wird die Summe der Differenzen maximal. Da beide Zeilenvektoren aber normiert werden, kann sich als maximale Summe der Differenzen nur Zwei ergeben. Wer’s nicht glaubt rechne mal ein Beispiel per Hand durch. Der Maximalwert der Chorddistanz beträgt also Wurzel von 2 gleich 1,414214 . Einfacher verständlich wird das Zustandekommen des Maximalwertes, wenn man sich noch einmal die Chorddistanz als Funktion des Cosinus vergegenwärtigt. Wenn zwei Zeilen nichts gemeinsam haben, ist der Anteil, zu dem die Länge des einen Zeilenvektors der Länge des anderen Zeilenvektors entspricht gleich Null. Dieser Grad der Entsprechung ist äquivalent mit dem Cosinus. Wenn in der Formel, die die Chorddistanz als Funktion des Cosinus zeigt, der Cosinus den Wert Null annimmt, dann ergibt sich als Maximalwert der Distanz: Wurzel aus 2 mal (1 minus 0) = Wurzel aus 2. Die Chorddistanz erreicht also bei prozentual völlig verschieden zusammengesetzten Fälle (Zeilen) einen Maximalwert von 1,414214 (die Wurzel aus 2). Bei völlig gleichartig zusammengesetzten Fällen wird sie 0. Die Chorddistanz wird umso geringer, je ähnlicher sich die Zeilenprozente (!) zweier Fälle sind. Vereinfacht gesagt benutzt die Chorddistanz eine Transformation der Zeilenprozente zur (Un-)Ähnlichkeitsmessung.
Die im folgenden Abschnitt beschriebene Metapher für das räumliche Verständnis der Chorddistanz orientiert sich an der letzten der hier erläuterten Formelvarianten, der von Legendre und Gallagher.
5. Zum geometrischen Verständnis der Chorddistanz
Zum Verständnis der Funktionsweise stellt man sich als jemand, der nicht auf abstraktes Denken in Zahlen trainiert ist – so wie ich zum Beispiel – , den Berechnungsablauf am besten mit räumlichen Metaphern vor. Eine hervorragende Einführung darin, wie man dies bei multivariaten Verfahren tun kann, bietet das schon mehrfach ziterte Lehrbuch von Thomas Wickens (ders. 1995).
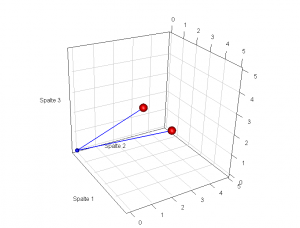
Bei der Chorddistanz genügt es, sich jede Tabellenzeile als Pfeil vorzustellen. Wie das? Nun jede Spalte der Tabelle sei eine Koordinatenspalte. Das bedeutet für jede Spalte – also jeden Typ – gibt es eine Koordinatenachse. Ein Zelleneintrag in der ersten Spalte – also die Häufigkeit von Typ 1 – entspricht also einer Koordinate auf dieser ersten Achse – quasi der “Typ-1-Achse”. Ein Zelleneintrag in der zweiten Spalte entspricht einer Koordinate auf der zweiten Achse usw. Bei bis zu drei Achsen kann man sich dies noch ganz gut vorstellen. Bei mehr als drei Achsen ist es zwar grafisch nicht mehr vorstellbar, die Berechnungen sind aber die gleichen. Die hier skizzierte Metapher benutzt eine Abundanztabelle mit zwei Fällen, Zeile 1 und Zeile 2, sowie drei Typen, pardon drei Spalten, pardon drei Achsen.
Zeichnet man die Zeilen in der besagten Art als Vektoren, so tut man dies in einem Koordinatensystem, dessen Achsen die Typen sind. Die Achsen treffen sich dabei alle im Nullpunkt und stehen senkrecht aufeinander, ganz so wie man Koordinaten kennt. Wenn Typ 2 bei Zeile 1 dreimal vorhanden ist, dann bedeutet das, man rückt 3 Einheiten auf der Achse 2 vor. Nun zeichnet man einfach für jede Zeile einen Pfeil (blaue Linie) vom Achsennullpunkt (dem blauen Punkt) zu den Koordinaten der Zeile (rote Punkte). Die beiden Zeilen z1 und z2 in der Grafik haben die Zellenwerte bzw. Koordinaten (2,4,1) und (1,3,2). D.h., in Zeile Z1 steht in der ersten Zelle der Wert 2, in der zweiten der Wert 4 und in der dritten der Wert 1. Typ 1 kommt also zweimal vor, Typ 2 viermal und Typ 3 einmal – analog Z2.
Die Spitzen der beiden Pfeile (Zeilenpunkte bzw. rote Punkte) sind sich umso näher, je ähnlicher sich die beiden Pfeile sind. Bei zwei Zeilen mit exakt denselben Werten lägen sie genau aufeinander.
Jetzt werden die Zeilen normiert, d. h. alle Einträge einer Zeile werden durch die Länge der blauen Linie – die Länge des Zeilenpfeiles bzw. des sog. Zeilenvektors geteilt. Man sagt auch, die Zeilenpfeile werden normalisiert. Die Länge eines solchen Pfeils bzw. Vektors wird als Norm bezeichnet. Da alle Zellen in einer Abundanzentabelle positive Werte enthalten, sind auch alle Ergebnisse dieser Division positiv. Die Länge der blauen Pfeile berechnet sich nach dem Pythagoras (vgl. zum Pythagoras 3.). Nur dass man diesmal einfach die Wurzel aus der Summe der quadrierten Typenhäufigkeiten zieht, um die einzelnen Pfeillängen zu erhalten. Die Anweisungen bis hierher lauten also: quadriere alle Zellenwerte einer Zeile einzeln – summiere sie – ziehe die Wurzal aus dieser Summe – teile die ursprünglichen Häufigkeiten einer Zeile durch diese Wurzel. Die Zahlen, die nach der Division der Typenhäufigkeiten durch die Vektorlänge in den Zeilen stehen, entsprechen immer noch den Koordinaten der Pfeilspitzen. Es sind auch weiterhin nur positive Werte. Diese Zahlen drücken die Anteile der einzelnen Spaltentypen an der Summe aller Zeileneinträge als Bruchteile der Länge des Zeilenpfeiles (Vektors) aus. Der Zeilenpfeil (Vektor) wurde quasi geschrumpft, denn eine Division kleinerer Werte (Typenhäufigkeiten) durch grössere (Summe aller Typenhäufigkeiten) ergibt kleinere Zahlen als die Ausgangswerte.
Wenn in einer Zeile alle Zellen eine gleichgrosse positive Zahl enthalten, dann tragen alle Spalten (Typen) gleichviel, also durchschnittlich, zur Zusammensetzung der Zeile bei. Bei der Berechnung von Zeilenprozenten hatte man gerechnet: Zellenwert durch Summe aller Zellenwerte einer Zeile. Mit Hundert multipliziert ergibt dies die Prozente. Die Berechnung des “Anteils” als Bruchteil der Länge benutzt eigentlich nur eine andere Bezugssumme. Da jeder Zellenwert bei Berechnung der Zeilenpfeillänge mit dem Pythagoras als Quadrat eingeht, entspricht der durchschnittliche Beitrag einer Zelle bei dieser Berechnung der Wurzel (!) aus Zeilensumme durch Spaltenanzahl. Bei der oben als Z2 (1,3,2) vorgestellten Zeile entspräche der durchschnittliche Zellenbeitrag 2 (Summe von 6 durch Spaltenzahl von 3 = 2). Als Zeilenprozent ausgedrückt also 100 * (2/6) = 33,3 %. Ausgedrückt als Bruchteil der Vektorlänge entspricht dies Wurzel aus (6 durch 3) also Wurzel aus 2. Die Chorddistanz basiert also genau genommen nur auf einer anderen Variante der Zeilenprozentberechnung. Nur dass eben diese Variante aufgrund ihrer Bezugssumme deutlich verbesserte rechnerische Eigenschaften aufweist, als die einfachen Zeilenprozentwerte zuvor.
Die “neuen” Koordinaten der Pfeilspitzen gewährleisten weiterhin, dass die Pfeile immer noch in die gleiche Richtung (!) wie zuvor zeigen, als die absoluten Typenhäufigkeiten die Koordinaten darstellten. Denn die Koordinaten wurden ja alle gleichmäßig “geschrumpft”, aber nicht in ihren gegenseitigen Bezügen verändert. Jeder Pfeil ist nach der Normalisierung nur noch eine Einheit lang (Länge=1). 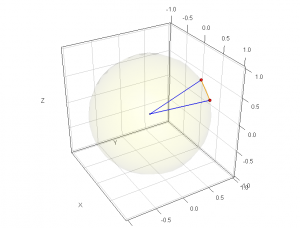 Die Zeilenpfeile liegen nun mit ihren Spitzen auf einer Kugel vom Radius 1. Warum eine Kugel? Nun, bei dem Beispiel mit den Zeilen Z1 und Z2 sind drei Dimensionen (drei Tabellenspalten) vorhanden. Eine Kugel ist ein dreidimensionaler Körper, bei dem alle Punkte auf seiner Oberfläche gleich weit von ihrem Mittelpunkt entfernt sind. Und die beiden Zeilenpfeilspitzen sind jetzt beide 1 lang, also 1 vom Achsenursprung entfernt. Ihre Spitzen müssen (!) also auf der Oberfläche einer Kugel mit Radius 1 liegen. Der Mittelpunkt der Kugel, der Punkt von dem aus die Zeilenpfeile (Vektoren) “starten”, liegt bei den Koordinaten (0,0,0). Bei der Kugel können die Pfeilspitzen nur auf dem Achtel der Kugeloberfläche liegen, das positive Koordinaten besitzt. Die Chorddistanz ist nun der Abstand (orange Linie) zwischen den beiden Pfeilspitzen. Und aufgrund der Standardisierung auf die Vektorlänge kann man jetzt einfach mit dem Pythagoras die Distanz zwischen den beiden Zeilen Z1 und Z2 berechnen. An diesem Punkt wird klar, warum die Chorddistanz metrische (euklidische) Eigenschaften besitzt, ohne von den Verzerrungen der Eukliddistanz betroffen zu sein (s. o. 2.6. und vgl. o. 3.). Geometrisch ausgedrückt entspricht die Chorddistanz also der Länge einer Sehne. Die Sehne geht durch die Kugel und schneidet sie an den Punkten Z1 und Z2. Auf dem Kugelachtel ist der grösstmögliche Abstand zweier Punkte der zwischen einem Punkt auf dem Kugeläquator und einem auf dem Kugelpol bzw. der Abstand zwischen zwei Punkten in den “Ecken” des Kugelachtels. Die Pfeile würden dann senkrecht aufeinander stehen – einer weist zum Pol, der andere zum Äquator der Kugel. Das Senkrecht-Aufeinander-Stehen zweier Zeilenpfeile (Vektoren) ist der visuelle Ausdruck einer kompletten Unähnlichkeit und wird auch als Orthogonalität bezeichnete. In einem solchen Fall haben die beiden Zeilen der Abundanzmatrix keine positiv besetzten Zellen gemeinsam.
Die Zeilenpfeile liegen nun mit ihren Spitzen auf einer Kugel vom Radius 1. Warum eine Kugel? Nun, bei dem Beispiel mit den Zeilen Z1 und Z2 sind drei Dimensionen (drei Tabellenspalten) vorhanden. Eine Kugel ist ein dreidimensionaler Körper, bei dem alle Punkte auf seiner Oberfläche gleich weit von ihrem Mittelpunkt entfernt sind. Und die beiden Zeilenpfeilspitzen sind jetzt beide 1 lang, also 1 vom Achsenursprung entfernt. Ihre Spitzen müssen (!) also auf der Oberfläche einer Kugel mit Radius 1 liegen. Der Mittelpunkt der Kugel, der Punkt von dem aus die Zeilenpfeile (Vektoren) “starten”, liegt bei den Koordinaten (0,0,0). Bei der Kugel können die Pfeilspitzen nur auf dem Achtel der Kugeloberfläche liegen, das positive Koordinaten besitzt. Die Chorddistanz ist nun der Abstand (orange Linie) zwischen den beiden Pfeilspitzen. Und aufgrund der Standardisierung auf die Vektorlänge kann man jetzt einfach mit dem Pythagoras die Distanz zwischen den beiden Zeilen Z1 und Z2 berechnen. An diesem Punkt wird klar, warum die Chorddistanz metrische (euklidische) Eigenschaften besitzt, ohne von den Verzerrungen der Eukliddistanz betroffen zu sein (s. o. 2.6. und vgl. o. 3.). Geometrisch ausgedrückt entspricht die Chorddistanz also der Länge einer Sehne. Die Sehne geht durch die Kugel und schneidet sie an den Punkten Z1 und Z2. Auf dem Kugelachtel ist der grösstmögliche Abstand zweier Punkte der zwischen einem Punkt auf dem Kugeläquator und einem auf dem Kugelpol bzw. der Abstand zwischen zwei Punkten in den “Ecken” des Kugelachtels. Die Pfeile würden dann senkrecht aufeinander stehen – einer weist zum Pol, der andere zum Äquator der Kugel. Das Senkrecht-Aufeinander-Stehen zweier Zeilenpfeile (Vektoren) ist der visuelle Ausdruck einer kompletten Unähnlichkeit und wird auch als Orthogonalität bezeichnete. In einem solchen Fall haben die beiden Zeilen der Abundanzmatrix keine positiv besetzten Zellen gemeinsam.
Zwei Punkte auf einer Kugeloberfläche kann man immer mit einer Schnittebene durch die Kugel erfassen. Man muss also bei der Berechnung des Abstandes mit dem Pythagoras nicht aus der Summe von drei Koordinatendifferenzen die Wurzel ziehen sondern nur aus zweien. Und dann ergibt sich als maximal möglicher Abstand die Wurzel aus der Summe von Eins zum Quadrat plus Eins zum Quadrat. Eins zum Quadrat ist Eins. Der maximal mögliche Abstand ist also die Wurzel aus Zwei gleich 1,414214. Dies ist der Grund, warum der Maximalwert für die Chorddistanz nicht grösser werden kann als Wurzel Zwei. Da der Cosinus eines 90°-Winkels gleich Null ist, wird bei zwei zueinander senkrechten Zeilenpfeilen (Vektoren) auch für die Formelvariante, die mit dem Cosinus arbeitet, der Maximalwert klar. Bei der “Cosinus-Variante” wird der Term in der inneren Klammer durch die Subtraktion von Null gleich 1: es verbleibt Wurzel aus (2*(1-0)) = Wurzel von 2 = 1,414214.
Na gut, aber wie sieht es aus, wenn die Typentabelle nicht 3 sondern 33 Spalten besitzt? Eigentlich ganz genauso. Die Kugel existiert dann eben nicht in drei sondern 33 Dimensionen. Jeder Punkt auf der Kugel ist dann in 33 Dimensionen gleich weit vom Kugelzentrum entfernt. Man hat es jetzt eben mit einer Kugel im Hyperraum zu tun. Und weiterhin bleibt die Maximaldistanz zwischen zwei Pfeilspitzen auf dieser Hyperkugeloberfläche die Wurzel aus Zwei.
Man sieht, die Chorddistanz basiert auf einer cleveren, eleganten und gut nachvollziehbaren Überlegung und hat rein gar nichts mit manchmal von rechenfeindlichen Archäologen geäusserten Vorurteilen gegenüber “Datenmanipulationen” zu tun, die die “guten” Rohdaten auf gespenstisch-hinterhältige Weise “verzerren” würden. Im Gegenteil, der Rechenweg “schützt” vor dem häufig ganz und gar nicht gesunden “gesunden Menschenverstand”, der nicht zu selten zu naiven, anstatt zu richtigen Ergebnissen kommt. Benutzt man die Chorddistanz anstatt des naiven Distanzmaßes Euklid, umgeht man konsequent die Verzerrungsgefahren durch das Typen-Abundanz-Paradoxon und das Doppel-Null-Problem.
6. Die Chorddistanz in R
Wie oben angemerkt ist es bei neuen Methoden sinnvoll, sie zum besseren Verständnis selbst “per Hand” in R nachzurechnen. Meine Notizen zur schrittweisen Chorddistanzberechnung in R waren der Ausgangspunkt für diesen Artikel. Alle Rechenanweisungen stehen zur Verfügung. Wer am liebsten alles von Grundauf selbst berechnet, kann die folgenden Befehle mit ein paar Schleifen verbinden, und so eine eigene Funktion für die Chorddistanz erstellen (zum Funktionen erstellen siehe den Artikel Potplot).
6.1. Berechnung per Hand
In diesem Abschnitt wird die Chorddistanz für das geomtrische Beispiel der Zeilen Z1 (2,4,1) und Z2 (1,3,2) in Einzelschritten mit einfachem R-Code ausgerechnet. Aus den Beispieldaten wird mit dem Befehl ‘matrix()’ eine Matrix erzeugt. Das erste Argument sind die Werte für die Zellen der Matrix, die mit ’c()’ als Verkettung angegeben werden. Innerhalb der Verkettung sind die einzelnen Einträge durch Kommata getrennt. Man beachte, dass die Matrix links oben beginnend nach unten (!) laufend aufgefüllt wird. Beim Ende einer Spalte springt R auf die nächste Spalte und beginnt wieder oben. Die beiden Zahlen nach dem ‘c()’, sind die Zeilenanzahl und die Spaltenanzahl der neuen Matrix.
(matrix(c(2,1,4,3,1,2),2,3)->mata)
Mit den names-Funktionen kann man Zeilen- (‘rownames()’) und Spaltenbezeichnungen (‘colnames() ‘ einer Matrix aufrufen und setzen – je nachdem, ob man nur aufruft, oder wie hier auch zuweist. Die Namen werden wegen der Anführungsstriche von R als Text angesehen. Wenn man die Anführungsstriche vergisst, sucht R nach einem R-Objekt diesen Namens, findet keines und beschwert sich. Da man mehrere Angaben hintereinander braucht, kommt wieder ‘c()’ zum Einsatz.
rownames(mata)<-c("z1", "z2")
colnames(mata)<-c("spalte1", "spalte2", "spalte3")
mata
Mit Hilfe der funktion ‘apply()’ wird auf das als erstes Argument gesetzte Objekt – hier die Matrix ‘mata’ – spaltenweise (Argument ‘MARGIN=2′) die anhand von ‘function (x)’ definierte Funktion angewendet. In diesem Fall hat man mit ‘x^2′ eine Funktion zum Quadrieren der Matrixeinträge definiert. Warum wird spaltenweise angewendet? Entgegen einem intuitiven Verständnis wird in R eine Matrix spaltenweise (!) durchlaufen. Wenn man ‘MARGIN=1′ gesetzt hätte, wäre das Ergebnis die transponierte Matrix der Quadrate geworden.
(apply (mata, MARGIN=2, function(x) x^2 ) -> masqa)
Die Wurzel aus der Summe dieser Quadrate ergibt den Vektor mit den Zeilenfpeillängen, also die Nenner in den Brüchen zur Chordtransformierung. Um bei einer Matrix die Zeilensummen zu berechnen, könnte man auch mit ‘apply()’ arbeiten, aber die Funktion ‘rowSums()’ ist unkomplizierter. Ihr Pendant für die Spalten hiesse … na? richtig ‘colSums()’. Beide Funktionen nehmen Matrizen oder Datentabelle (‘data.frame’) als Objekte. ‘sqrt()’ steht natürlich für das englische “square root”, also Quadratwurzel.
(sqrt( rowSums(masqa)) -> nenna)
Das Teilen der Zeilenwerte durch den entsprechenden Eintrag des Vektors ‘nenna’ erzeugt die chord-transformierten Werte der beiden Zeilen. Die Zeilen werden durch die Indizierung der Matrix ‘mata’ aufgerufen. In den eckigen Klammern steht vor dem Komma die Nummer der verwendeten Zeile. Wenn nach dem Komma nichts steht, dann werden alle Spalten verwendet. Da das Objekt ‘nenna’ nur ein Vektor ist, wird hier nur mit der Position des Eintrags im Vektor indiziert.
(mata[1,]/nenna[1]->py1)
(mata[2,]/nenna[2]->py2)
Die Objekte ‘py1′ und ‘py2′ sind wieder Vektoren. Sie enthalten die von Legendre und Gallagher entdeckte multivariat-metrische Repräsentation der Abundanzen. Auf diese transformierten Werte wird der Pythagoras angewendet.
(sqrt(sum( ( py1-py2 )^2))->hand_d)
Das Ergebnis ist die von Hand ausgerechnete Chorddistanz. Zum Beweis wird daneben eine bestehende Funktion verwendet. Die Funktion wird im nächsten Unterabschnitt erläutetr s. u. 6.2.).
install.packages("vegan")
library(vegan)
(dist(decostand(mata, "norm"))->auto_d)
Die Funktion ‘all.equal()’ vergleicht zwei R-Objekte auf Gleichheit aller sich entsprechender Einträge. Da ‘auto_d’ ein Objekt der Klasse ‘dist’ (für ‘distance’) ist,
class (auto_d)
die Funktion ‘all.equal()’ damit aber Probleme hat, wird es kurzerhand durch Anwendung der Verkettungsfunktion ‘c()’ in einen Vektor verwandelt.
all.equal( c (auto_d), hand_d )
6.2. Einlesen einer Abundanztabelle aus einem “Spreadsheet”
Grundsätzlich lassen sich Daten auf viele verschiedene Arten nach R Einlesen (siehe hierzu den Artikel “Import von Daten”). Hier wird von einer “quick-and-dirty-Situation” ausgegangen, bei der man bereits eine OpenOffice-Calc-Tabelle vorliegen hat (na schön, EXCEL geht genauso), die beispielsweise zuvor aus einer Publikation abgetipt wurde. In der ersten Spalte stehen ab der zweiten Zeile die Namen der Fälle und in der ersten Zeile stehen ab der zweiten Spalte die Namen der Typen bzw. Merkmalsausprägungen der Nominalvariablen. In der ersten Zelle links oben steht nichts. Man markiere die gesamte Tabelle von der ersten Zelle links oben bis zur letzten Zelle rechts unten und kopiere sie mit dem sog. Guttenberg-Griff “STRG+c” in den Zwischenspeicher. Der folgende Befehl liest eine derartige Tabelle aus dem Zwischenspeicher nach R als Datentabelle ein. Das erste Argument liest den Zwischenspeicher (“clipboard”) aus. Das Argument ‘header=TRUE’ besagt, es gibt eine Kopfzeile (“header”) mit Spaltenüberschriften. Und schließlich wird mit dem Argument ‘row.names=1′ – nicht zu verwechseln mit der Funktion ‘rownames()’ (!) – angegeben, dass die erste Spalte die Namen der Fälle enthalte.
read.table("clipboard", header=TRUE, row.names=1)->abudat
Zur besseren Verarbeitung wird die Datentabelle, die ja schon eine Abundanzmatrix ist, in ein R-Matrix-Objekt verwandelt.
as.matrix(abudat)->abu
Das Objekt ‘abu’ ist eine Matrix, deren Zeilennamen den Fallnamen und deren Spaltennamen den Typennamen entsprechen. Den Aufbau eines R-Objektes zeigt der Befehl ‘str()’ (für “structure”).
str(abu)
Jetzt kann die Erstellung der Distanzmatrix beginnen.
6.3. Berechnung mit dem Paket ‘vegan’
Das R-Paket ‘vegan’ wird von Jari Oksanen (*1954), einem Professor für Pflanzenökologie an der Universität von Oulu/Finnland, stetig weiterentwickelt und besitzt eine eigene Netzpräsenz. Es ist aufgrund seiner Vielseitigkeit und den zahlreichen Tutorien zu den verschiedenen Methodengebieten die Königin der R-Pakete für multivariate Statistik – aus meiner Sicht. Das Paket kann man entweder direkt in R installieren, wenn der benutzte PC online ist, oder hier direkt herunterladen. Der folgende Code installiert das Paket direkt online aus dem Internet, lädt es in R und gibt auf dem Bildschirm das Zitat aus. Wie andernorts bemerkt muss man R und die verwendeten Pakete zitieren.
install.packages("vegan")
require(vegan)
citation("vegan")
Die Chord-Distanz erhält man im Paket ‘vegan’ über den Umweg der Funktion ‘decostand()’. Sie transformiert eine Abundanztabelle auf verschiedene Weisen. Das Argument “norm” erzeugt einen Zwischenschritt für die Chorddistanzberechnung. Es teilt alle Zelleinträge einer Zeile durch die Wurzel aus der Summe der quadrierten Zellenwerte einer Zeile (zur Berechnung s. o.). Dies ergibt die chord-transformatierte Matrix. Der Vorgang wird manchmal auch als standardisieren “auf Zeilenvektorlänge” oder als zeilenbezogene (Vektor-)Normalisierung bezeichnet, deshalb die Abkürzung “norm” als Argumenteintrag.
decostand(abu, "norm")-> abu.cho.pre
Die transformierte Abundanzmatrix ist zunächst noch eine vollständige rechteckige Matrix, keine Dreiecksmatrix, wie bei Distanzberechnungen üblich. In diesem Zustand ist das R-Objekt eine metrisch-multivariate Repräsentation der Abundanztabelle. Es enthält die Koordinaten der Zeilenpunkte auf dem Kugelachtel im Hyperraum (s. o. 5.).
str(abu.cho.pre)
Die euklidischen Distanzen dieser chord-transformatierten Matrix ergeben die eigentliche Dreiecksmatrix mit den Chorddistanzen der Objekte.
dist(abu.cho.pre )-> abu.veg.cho
str(abu.veg.cho)
Möchte man die Distanzmatrix in anderen Programmen weiter verwenden, kann es sein, dass dort eine rechteckige und keine dreieckige Distanzmatrix erwartet wird. Dann wiederholt man die Distanzerzeugung und setzt die Argumente ‘diag=’ und ‘upper=’ beide auf TRUE. Jetzt wird eine rechteckige Matrix erzeugt. Zusätzlich wird mit dem Befehl ‘as.matrix()’ das Ergebnis gleich in die Klasse R-Matrixobjekt überführt.
as.matrix(dist(abu.cho.pre, diag=TRUE, upper=TRUE ))-> abu.exp.cho
str(abu.exp.cho)
Jetzt werden nocheinmal sicherheitshalber die Bezeichnungen für Zeilen und Spalten der Distanzmatrix aus der ursprünglichen Abundanzmatrix übernommen.
rownames(abu.exp.cho)
colnames(abu.exp.cho)
Das Ergebnis ist bereit für den Export.
Die zuerst erzeugte Dreiecksdistanzmatrix ‘abu.veg.cho’ ist als Objekt der Klasse ‘dist’ nicht einfach exportierbar.
class(abu.veg.cho)
Mit dem folgendem Code wird die Chorddistanzmatrix als Diagonalmatrix exportiert, also gefüllt mit Nullen in der “überflüssigen” Dreieckshälfte. Zunächst wird eine mit Nullen gefüllte Matrix der gleichen Größe dadurch erzeugt, dass man die vollständige, in ein R-Matrix-Objekt verwandelte, Chorddistanzmatrix von sich selbst abzieht.
abu.exp.cho-abu.exp.cho->abu.dia.cho
Jetzt kommt eine Schleife mit zwei Ebenen. In der ersten Ebene wird die Schleife entlang des Schleifenzählers i durchlaufen. ‘for (i in’ gibt also an, mit welchem Wert gestartet werden soll und bei welchem geendet wird. Als Ordnungsnummer des letzten Durchlaufes der ersten Ebene wird die Zeilenanzahl der Distanzmatrix gewählt ‘nrow(abu.exp.cho)’. Man achte darauf, dass nach der Schleifendefinition geschweifte Klammern ‘{‘ den Anfang und das Ende ‘}’ der Schleife definieren. Da es hier zwei Schleifenebenen gibt, gehen zweimal geschweifte Klammern auf und zu.
for (i in 1:nrow(abu.exp.cho))
In einem Durchlauf der ersten Ebene wird jetzt wiederum eine ganze Schleife der zweiten Ebene durchlaufen. Der Schleifenzähler ist diesmal j und läuft von 1 bis zur Spaltenzahlen der Distanzmatrix.
{for (j in 1:ncol(abu.exp.cho))
In jedem Durchlauf der untersten Schleifenebene wird einmal mit ‘ifelse()’ gefragt, ob ein Objekt eine Eigenschaft erfüllt. Die Funktion ‘ifelse()’ nimmt drei Argumente. Zuerst kommt die logische Abfrage. Hier ist es die Frage, ob die Schleifenzahl der unteren Ebene grösser als die der oberen Ebene ist’j>=i’. Es folgt, was im Fall einer positiven Beantwortung der logischen Frage zu tun ist. Hier wird bei Eintreten der Bedingung in eine Zelle der mit Nullen gefüllten Matrix eine Null geschrieben. Die Zelle wird durch die beiden Schleifenzähler identifiziert. Wenn die logische Frage den Wert FALSE ergibt, dann wird der Zellenwert aus der quadratischen Distanzmatrix in die Nullen-Matrix geschrieben. Mit anderen Worten, wenn beim Durchlauf der ersten und zweiten Schleifenebene die beiden Schleiferzähler i und j eine Position auf der Matrixdiagonalen oder rechts oberhalb davon definieren – also wenn j grösser oder gleich i ist-, wird die Zelle der bearbeiteten Matrix ‘abu.dia.cho’ gleich Null, ansonsten erhält sie den Distanzwert zugewiesen.
{ifelse(j>=i, abu.dia.cho[i,j]<-0, abu.dia.cho[i,j]<-abu.exp.cho[i,j]) }}
rownames(abu.dia.cho)
colnames(abu.dia.cho)
Man könnte sofort einen Exportbefehl (s. u.) verwenden, aber aus didaktischen Gründen folgt jetzt ein bisschen Code zur Kommunikation zwischen R und dem PC. Man überprüft zunächst den Pfad des momentanen Arbeitsverzeichnisses,
getwd()
wechselt auf die oberste Ebene,
setwd("C:/")
erzeugt dort ein eigenes Arbeitsverzeichnis,
dir.create("99_DATA")
überprüft das Ergebnis,
dir()
und setzt den Pfad des Arbeitsverzeichnisses auf diesen neuen Ordner.
setwd("C:/99_DATA")
Jetzt wird mit dem Befehl ‘write.table()’ die rechteckige Distanzmatrix ‘abu.exp.cho’ als Datei namens “chorddist.txt” im .txt-Format exportiert. Die Diagonalmatrix ‘abu.dia.cho’ wird als Datei namens “chorddistdiag.txt” ebenfalls im .txt-Format ausgeschrieben. Durch das Argument ‘row.names=TRUE’ werden die Zeilenbezeichnungen des R-Objektes mit in die Datei geschrieben. Das Argument ‘quote=FALSE’ verhindert, dass in der Datei alle Texteinträge in Apostrophen stehen.
write.table(abu.exp.cho, row.names=TRUE, quote=FALSE, "chorddist.txt")
write.table(abu.dia.cho, row.names=TRUE, quote=FALSE, "chorddistdiag.txt")
Ein abschliessende Überprüfung des Erfolges:
dir()
Die eine oder andere Distanzmatrixvariante sollte sich in viele Programmen importieren lassen. Wenn es Probleme bei der Erkennung des Dezimalpunktes geben sollte – wer hat hier was von Excel gesagt? ![]() – , setzt man beim Schreibebefehl noch das Argument für das Dezimaltrennzeichen ‘dec=”,” ‘. Es ist natürlich auch möglich, die Datei später im Texteditor zu öffnen und die Dezimalpunkte mittels “Suchen und Ersetzen” durch Kommata zu ersetzen.
– , setzt man beim Schreibebefehl noch das Argument für das Dezimaltrennzeichen ‘dec=”,” ‘. Es ist natürlich auch möglich, die Datei später im Texteditor zu öffnen und die Dezimalpunkte mittels “Suchen und Ersetzen” durch Kommata zu ersetzen.
6.4. Berechnung mit anderen Paketen
Eine Reihe anderer Pakete geben an, die Chorddistanz zu berechnen. Eine Überprüfung zeigte jedoch, dass hier teilweise die Formeln anders als in der Definition von Orloci verstanden werden, und folglich auch andere Distanzwerte berechnet werden. Irreführendes, nicht auf Definitionen achtendes Vorgehen gibt es also nicht nur in der Archäologie ![]() .
.
Positiv überprüft sind bis jetzt nur zwei Pakete. Das eine ist das Paket ‘rioja’. Hier ist aber zur Zeit die Funktion ‘paldist()’ noch nicht stabil und kann zum Absturz von R führen. Als Argument müsste man ‘chord.t’ für “true chord distance” setzen.
Nach einer nicht erschöpfenden Überprüfung bietet m. W. momentan einzig das Paket ‘proxy’ eine stabile Alternative zur Berechnung in ‘vegan’.
install.packages("proxy")
require(proxy)
Das Paket ‘proxy’ hat aber die aufdringliche Eigenheit, die Stammfunktion des Basispaketes für Distanzberechnungen ‘dist()’ mit einer eigenen Funktion gleichen Namens zu überschreiben. Ein bisschen Bescheidenheit und Kompatibilität hätte hier nicht geschadet. Das Ergebnis ist jedenfalls wie
erwartet. Man beachte (!), wenn ‘proxy’ in R geladen ist, berechnet eine Eingabe des Befehls ‘dist()’ keine euklidische Distanz der Koordinatentabelle.
dist(abu, method="chord")-> abu.pro.cho all.equal(c( abu.pro.cho), c( abu.veg.cho))
Der Vergleich mit dem über ‘vegan’ erzeugten Ergebnisobjekt belegt die definitionsgemäße Ergebnisgleichheit. Das Paket ‘proxy’ bietet übrigens noch zahlreiche andere Distanz- und Ähnlichkeitsmaße an, etwa die Ochiai-Ähnlichkeit für Präsenz-Absenz- bzw. Binärvariablentabellen. Einen Überblick über die mit ‘proxy’ berechenbaren Maße gibt der Befehl:
summary(pr_DB, "long")
Zu den meisten Maßen finden sich Definitionen und Erörterungen bei Legendre und Legendre (1998, Kap. 7) sowie Kindt und Coe (2005, )
7. Zusammenfassung Chorddistanz
Die Chorddistanz ein Distanzmaß zur Messung der Unähnlichkeit der Zusammensetzung von Fällen (Zeilen) einer Abundanzmatrix (Typenvergesellschaftungstabelle). Sie erreicht einen Maximalwert von 1,41414 bei komplett verschiedener Zusammensetzung der verglichenen Fälle und einen Minimalwert von 0 bei identischen Zusammensetzungen. Die Berechnungen beruhen auf einer Transformation der Zeilenprozentwerte. Ob zwei in Bezug auf die Zeilenprozente gleichartigen Fälle sich bei der Gesamtsumme der erfassten Objekte unterscheiden (Zeilensummen), kann sie nicht messen. Als asymmetrisches Distanzmaß bewertet sie Absenz anders als Präsenz und ist deshalb für die Archäologie besonders interessant. Als metrisches Distanzmaß besitzt sie euklidische Eigenschaften. Daher sind bei ihr alle Arten von Rechenoperationen zulässig. So können sämtliche, auf Distanzmatrizen aufbauenden, statistischen Methoden sie verwenden. Im Gegensatz zur Eukliddistanz führt sie nicht zu Verzerrungen und fehlerhaften Abbildungen der multivariaten Information einer Abundanzmatrix.
8. Literatur zur Chorddistanz
R. Kindt/R. Coe, Tree diversity analysis. A manual and software for common statistical methods for ecological and biodiversity studies. Nairobi: World Agroforestry Centre (ICRAF)(Nairobi 2005). [pdf-download des Online-Buches].
P Legendre/E. Gallagher, Ecologically meaningful Transformations for Ordination of Species Data. Oecologia 129, 2001, 271–280. DOI 10.1007/s004420100716 [pdf-download des Artikels].
P. Legendre/L. Legendre, Numerical Ecology. Developments in Environmental Modelling 20 (Amsterdam 1998) [Eintrag im world catalogue].
L. Orloci, An agglomerative Method for Classification of Plant Communities. Journal of Ecology 55, 1967, 193-205 [pdf-download des Artikels].
ders., Multivariate Analysis in Vegetation Research (Den Haag 1978). [Eintrag im world catalogue].
Th. Wickens, The Geometry of multivariate Statistics (Hillsdale/NY 1995) [Eintrag im world catalogue].
9. Überblick über verwendete R-Befehle
Befehl # Funktion § Zielobjekt * Paket
all.equal # vergleicht den Inhalt zweier R-Objekte § R-Objekt * base
apply # wendet Funktion zeilen/spaltenweise auf R-Objekt an § Datentabelle oder Matrix * base
as.matrix # verwandelt ein geeignetes R-Objekt in eine R-matrix § Datentabelle oder Distanzmatrix * base
colnames # weist oder zeigt die Spaltennamen von R-Objekten § Datentabelle oder Matrix * base
colSums # bildet die Spaltensummen eines R-Objekten § Datentabelle oder Matrix * base
class # gibt die Klasse eines R-Objektes aus § R-Objekt * base
decostand # transformiert die Werte einer Abundanzmatrix § Datentabelle oder Matrix * vegan
dir # Listet Dateien im Arbeitsverzeichnis § * base
dist # berechnet die Eukliddistanz der Zeilen einer Tabelle § Daten-, Kreuztabelle oder Matrix * stats
file.choose # Datei auswählen § [nur mit Einlesebefehl sinnvoll] * base
for (i in [Anfang]:[Ende])# Programmierschleife § [gefolgt von zu wiederholdender Aktion] * base
getwd # fragt Arbeitsverzeichnispfad ab § * base
ifelse # führt Alternativen nach logischer Abfrage aus § R-Objekt [Programmierung] * base
install.packages # installiert Paket von der Befehlszeile aus § Paketname in Anführungsstrichen # utils
library # lädt Paket, synonym zu ‘require()’ § Paketname als Text* base
matrix # erzeugt ein Zahlenfeld § Füllung des Zahlenfeldes, Zeilen- und Spaltenanzahl * base
ncol # gibt die Spaltenzahl eines R-Objektes aus § Datentabelle, Matrix oder Kreuztabelle * base
nrow# ergibt die Zeilenzahl eines R-Objekten § Datentabelle oder Matrix * base
read.table # Einlesen von Daten in eine R-Datentabelle § Rohdatendatei * utils
rep # wiederholt Objekt § Zu wiederholendes Objekt und Wiederholungsanzahl * base
require # lädt Paket, synonym zu ‘library()’ § Paketname als Text* base
rownames # weist oder zeigt die Zeilennamen von R-Objekten § Datentabelle oder Matrix * base
rowSums# bildet die Zeilensummen eines R-Objekten § Datentabelle oder Matrix * base
setwd # setzt Arbeitsverzeichnispfad § * base
sqrt # zieht die Wurzel § Vektor, Datentabelle oder Matrix * base
str # zeigt Aufbau eines R-Objektes § R-Objekt * utils
summary # erzeugt zusammenfassende Informationen zu einem R-Objekt § R-Objekt * base
write.table # Export einer R-Datentabelle in eine Datei im .txt-Format§ R-Datentabelle * utils